
1. 다음의 합성수를 소수로 분해하여라.
1) 140, 2) 450
소인수분해는 마지막 소수가 나올 때까지 나누기를 반복하면 된다, 그래서 위의 합성수를 소인수분해하면

2. 합성수 360을 소인수분해하면 2^a * 3^b * 5^c가 나오는데, 이때 a+b+c를 구하여라
먼저 합성수 360을 소인수분해하면 2^3 * 3^2 * 5가 나온다. 그래서 a=3, b=2, c=1이므로, a+b+c=6이다.

3. 숫자 200에 어떤 수를 곱하여 제곱수를 만들려고 한다, 이때 곱할 수 있는 가장 작은 수를 구하시오.
먼저 제곱수란 어떤 자연수의 제곱 형태를 말하는데, 예를 들어 자연수 4, 9, 16, 25, 36 ... 등이 제곱수이다. 그래서 소인수분해를 해서 나온 소수들을 제곱(x^2) 형태로 만들면 된다.

그래서 일단 숫자 200을 소인수분해하면 2^3 * 5^2이 나오는데, 제곱 형태로 만들면 2^2 * 2 * 5^2으로 바꿀 수가 있다. 그럼 해당 수식을 완전한 제곱 형태로 만들려면, 가운데에 있는 2에 어떤 수를 곱하여 제곱 형태로 만들어야 하는데, 곱할 수 있는 가장 작은 수는 숫자 2이다.

4. 숫자 396에 어떤 수를 나누어 제곱수를 만들려고 한다. 이때 나눌 수 있는 가장 작은 수를 구하시오.
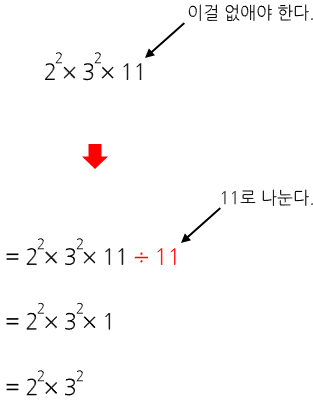
위의 문제와 비슷한데, 일단 숫자 396을 소인수분해하면 2^2 * 3^2 * 11이 나온다. 그런데 여기서는 "나누기를" 하는 것이므로, 해당 수식을 완전한 제곱 형태로 만들려면 11을 없애야 한다, 그래서 나눌 수 있는 가장 작은 수는 11이다.
'그래픽스 > 수학 물리' 카테고리의 다른 글
| 소인수분해로 약수의 개수 구하는 문제 풀이 (0) | 2024.08.28 |
|---|---|
| 소인수분해로 약수의 개수 구하는 법 (0) | 2024.08.28 |
| 소인수분해란? (0) | 2024.08.28 |
| 소수와 합성수란? (0) | 2024.08.27 |
| 절댓값 (absolute value) (0) | 2024.08.27 |
