수의 체계
숫자를 집단화 시켜 묶어 놓은 것이다.

정수
정수 (integer)는 크게 3가지로 구분 되어 있다. 양의 정수, 0, 음의 정수.
양의 정수는 자연수(natural number)라고도 하며 우리가 흔히 쓰는 숫자인 1,2,3,4 ... 와 같은 숫자를 말하며 양수라고도 한다.
음의 정수는 마이너스 값을 가진 정수다. -1,-2,-3,-4 ...와 같은 숫자를 말하며 음수라고도 한다.
0은 양의 정수와 음의 정수 가운데에 있는 아무것도 아닌 값이다.
유리수
정수가 아닌 수에는 소수가 있으며 이 소수는 크게 두 가지로 구분이 된다, 유한소수와 무한소수.
유환소수는 쉽게 볼 수가 있다, 0.1, 0.2 또는 0.34, 0.567 ... 등등 분수로 나타내면 아래와 같다

분수로 딱 맞아 떨어진다 하더라도 무조건 유한 소수인것은 아니다, 분수의 아래쪽 부분, 즉 분모가 소인수 분해를 하여 2나 5로 나누어 떨어져야한다, 그게 아니라면 무한소수다 대표적인 숫자로 3,7,11,13,17 등이 있다.
다음 분수 값을 소수로 나타낼려면


이렇게 규칙이 있는 소수는 순환소수, 그리고 규칙조차 없는 소수는 비순환소수다, 위의 나온 순환소수를 간단하게 표현하자면

이렇게 규칙이 있는 숫자 ㅟ에 점을 찍은 것을 순환 마디라고 한다. 이 순환소수는 다음과 같이 소수 첫째 자리나 둘째 자리부터 규칙이 없어도 순환마디로 표기할 수 있다.
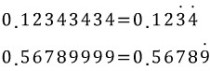
무리수
비순환소수를 무리수라고 한다 즉, 합리적이지 못한, 비율로 나타낼 수 없는 수이다.
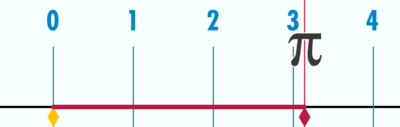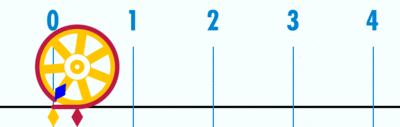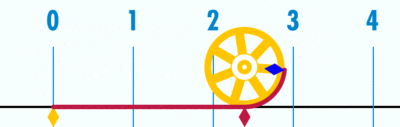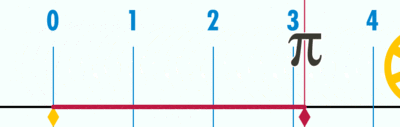
보통 초등학교에선 3.14라고 배우고 중학교 부터 그리스 문자 π(파이)를 사용해서 나타내지만 두 개를 쓸 수 없는 이유는 아직까지도 인간의 기술로 원주율의 값을 정확하게 계산하지 못했기 때문이다, 정확하게는 3.1415926535로 계속 계산 중인데 이렇게 규칙 없고 끊임없이 나가는 숫자를 무리수라고 한다 .
원주율 외에도 간단한 무리수가 또 있다, 바로 제곱근에 가장 기초가 되는 루트 2이다.
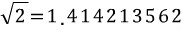
이렇게 유리수와 무리수 집단을 묶은 것을 실수라고 한다. 실수는 실체가 분명한 수, 진짜 숫자이다 그래서 영어로도 real number이라고 쓴다.
'그래픽스 > 수학 물리' 카테고리의 다른 글
| 절댓값 (absolute value) (0) | 2024.08.27 |
|---|---|
| 제곱근과 실수 (0) | 2024.08.27 |
| 좌표계 (Coordinate system)와 수학적 공간 (Mathematical space) (1) | 2024.05.02 |
| 동차 좌표계란? (0) | 2024.05.02 |
| 투영 행렬 유도와 ndc (0) | 2024.05.02 |
