투영변환이란
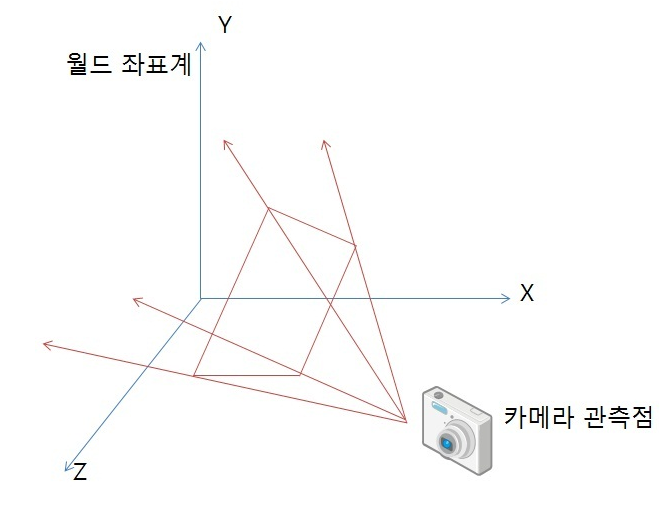
실세계의 한 점 Q = (x, y, z)는 3차원의 점이다.
이 점이 투영 스크린상의 한 점 (x, y)의 2차원으로 변환되는 것이 투영 변환이다.
투영 변환을 위해서는 동차 좌표계를 사용하는 것이 편리하다.
동차 좌표계란?
3D에서는 기본적으로 3차원 좌표계이지만 어떤 목적으로 4차원으로 확장이 가능하다.
어떤 목적을 위해 한 차원의 좌표(n) 을 추가한 좌표 (n+1)로 표현을 하는 것을 동차 좌표계라고 한다.
ex) 4차원 좌표 =(x,y,z,w) => x/w , y/w , z/w
투영행렬에서 동차좌표를 이용하는 이유
시점으로 보이는 점들의 위치가 중요한 것이 아니라 시점으로 부터의 방향이 중요하기 때문에 동차좌표를 사용한다.
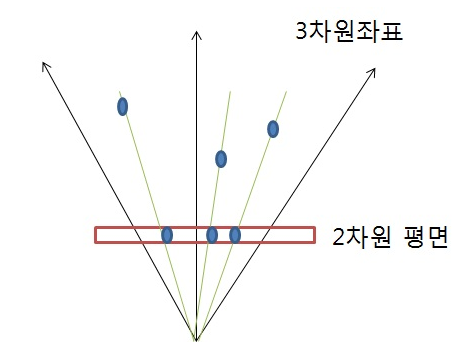
투영 행렬을 위 그림으로 나타내면 3차원의 점들이 2차원 평면의 빨간 네모 안에 다 모이는 것을 확인 할 수 있다.
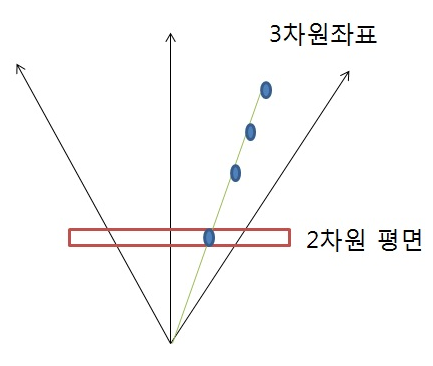
서로 다른 3차원의 점도 2차원에 투영 될 때는 하나가 되버린다는 점을 알 수 있다. 따라서 시점으로부터의 방향이 중요한 것을 알 수 있다.
3D에서의 동차좌표
동차좌표계가 있음으로써 행렬간의 이동을 곱셈으로 표현이 가능하다. 이동, 크기, 회전을 모두 담은 행렬은 최소 4*4 행렬일 수 밖에 없다. 이 행렬과 정상적인 연산을 하기 위해서는 백터도 행렬이므로 1x4 , 4x1 행렬 형태를 맞춰야 한다.
포인트(w=1)과 벡터(w=0)을 가늠할 수 있는 기준이 되기도 한다.
동차좌표는 방향과 점을 구분시켜준다. x,y,z의 3차원 좌표계 구조체는 점인지 방향인지 구분이 모호하다. 따라서 동차 좌표계가 포함된 4차원 좌표계로 표현하면 0은 방향 1은 위치로 표현 할 수 있다.

'그래픽스 > 수학 물리' 카테고리의 다른 글
| 실수, 유리수, 무리수, 정수, 자연수, 순환소수, 비순환소수란? (0) | 2024.08.27 |
|---|---|
| 좌표계 (Coordinate system)와 수학적 공간 (Mathematical space) (1) | 2024.05.02 |
| 투영 행렬 유도와 ndc (0) | 2024.05.02 |
| 지수의 밑변환 공식, 로그의 밑변환 공식 - 개념, 유도, 적용 (0) | 2024.04.24 |
| 로그(log) 계산 공식 (상용로그, 자연로그) 총정리 (0) | 2024.04.24 |
