일반적인 공간인 '유클리드 공간(Euclidean space)'에서 보통 어떤 수학/물리적 문제를 다룬다. 사실 어떤 물리적 사건을 표현할 때에 '어떤 공간을 사용하는가'는 '어떤 좌표계를 사용하는가'만큼이나 중요하다. 심지어 좌표계와 공간(space)을 헷갈려하는 학생들 또한 매우 많다.
우선 공간부터 살펴보자. 아주 옛날인 기원전 300년 쯤 고대 그리스의 유클리드는 기하학을 연구하였고, 그가 정리한 5가지 원칙을 만족하는 아주 기본적인 공간을 유클리드 공간이라 부른다. 아래 그림은 우리에게 매우 익숙한 3차원 유클리드 공간이다.

직선(line)은 1차원 유클리드 공간의 예이다. 이러한 직선은 어떠한 '단위간격(unit interval)'로 측정/표현할 수 있다. 아무렇게나 '단위간격'을 정한 후, 원점에서 양쪽 방향으로 무한히 '단위간격'을 이어 붙이면 직선이 된다. 이러한 '단위 간격'을 정하는 것이 어떤 공간에서 '좌표계(coordinate system)'를 설정하는 것의 시작이다
평면(plane) 또한 2차원 유클리드 공간의 예이다. 평면에서의 측정/표현을 위해선 '단위간격'외에도 '단위면적(unit square)'가 필요하다. 이러한 유클리드 평면 상에서 원, 삼각형, 사각형 들의 물체는 변형(deformation)없이 이동이 가능하다 (생각해보면 당연하다). 또한 평행한 두 선은 영원히 만나지 않는다. 유클리드 공간에서 삼각형 내각의 합은 언제나 180도이다(아래 그림의 평면).

이러한 유클리드 공간에서는 주로 직교 좌표계(Cartesian coordinate system)가 사용된다. 데카르트 좌표계라고도 부른다. 우리가 고등학교 때 많이 보았던 x축 y축으로 이루어진 좌표계가 이것이다. 직각으로 만나는 두개의 두 직선(line)으로 구성된 좌표계이다. 물론 극좌표계(polar coordinate system)등 다른 좌표계를 사용해도 된다. 또한 아래 그림처럼 이러한 좌표계들은 서로 변환이 가능하다.

하지만 실제 우주 상에는 중력 등의 영향으로 이러한 이상적인 유클리드 공간은 존재하지 않는다. 1900년대 초 아인슈타인이 약관의 나이로 유명한 일반상대성이론을 만들 때, 유클리드 공간이 아닌 '비유클리드 공간'으로 이론을 펼쳐나갔다.
'비유클리드 공간' 중 가장 간단한 것은 '구면 기하학'이다. 위의 회색 그림처럼 평면 대신 '구의 표면'을 기준으로 하는 것이다 (마치 지구처럼). 이는 가끔 '리만 기하학'이라고 불리기도 한다.
구(sphere)는 3차원이지만 '구표면'은 평면(plane)처럼 2차원이다. 하지만 평면과 달리 '무한히' 퍼지지 않고 일종의 '닫힌'계(system)이다. 또한 측정/표현법 또한 다르다.이러한 '구표면'에서 유클리드 공간처럼 '단위 간격'을 만드려면, 직선이 아니고 '휜(curved) 선'이여야 하는데, 이렇게 정의하면 너무 복잡하므로 '미분 기하학(differential geometry)'이 도입되었다. 이름은 어렵지만 그리 어렵지 않다. 그냥 '매우 작을 때'를 가정한 것이다. 비유클리드 공간인 '구표면'도 아주 작은 부분을 확대해서 보면, 유클리드 공간처럼 보인다는 것이다. 마치 우리가 지구라는 '구표면'에 살지만 (정확한 구는 아니지만), 삼각형을 그렸을 때 지구 크기에 비해 너무 작으므로 내각의 합이 180도라 가정할 수 있는 것과 같다.

위의 그림은 '비유클리드 공간'인 구표면(지구)에서 삼각형을 그린 모습이다. 크게 그리니 삼각형의 내각의 합이 무려 230도이지만, 아주 작은 곳에선 180도로 근사(approximation)가 가능하다. 그림으로(기하학적으로) 이해했으니 수학으로 나타내보자.
2차원 유클리드 공간인 평면에서는 직각삼각형에 대한 그 유명한 '피타고라스 정리가 성립한다.
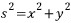
하지만 2차원 비유클리드 공간인 '구표면'에서는 '피타고라스 정리'가 성립하지 않는다.
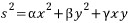
하지만 마찬가지로 아주 작은 부분에서는 '피타고라스 정리'가 다시 성립한다.
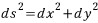
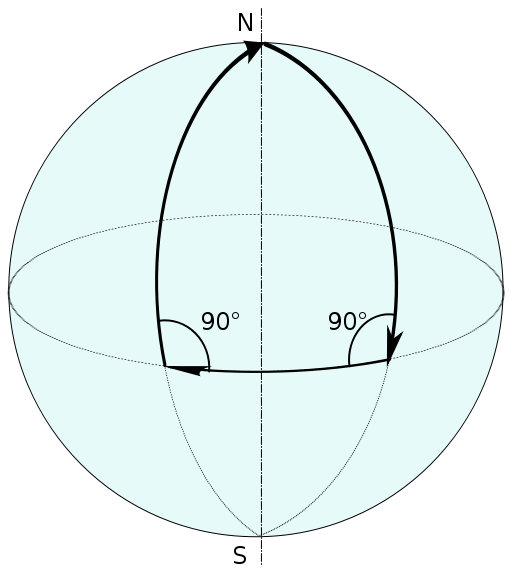
여기서 ds, dx, dy는 differential length(미소 길이)이다. 이렇듯 비유클리드 공간에서도 '매우 작다'는 가정을 거쳐서 마치 유클리드 공간처럼 사용하곤 한다. '구표면'에서는 마치 평면(plane)처럼 원, 삼각형 등의 도형이 변형없이 이동할 수 있다. 하지만 '구표면'에서는 평행하는 두 직선은 존재하지 않으며 항상 어떠한 점에서 만나게 된다. 따라서 '구표면'과 같은 공간에서는 '직교(Cartesian) 좌표계'는 존재하지 않는다. 아래 그림을 보면, 두 선 모두 적도와 90도로 직각이여서 처음엔 평행하지만 결국 한 곳(북극점)에서 만나게 된다.
이번에는 '달걀표면'을 떠올려보자. '구표면'처럼 닫혀 있으며 역시 2차원이다. 하지만 여기서는 도형들이 변형없이 이동할 수 없다. 수학적 용어로 쓰면 '합동'이나 '닮음'이 불가능하다. 마찬가지로 아주 아주 작은 부분에서는 마치 평면처럼 보이므로, 유클리드 공간처럼 쓸 수 있다. 하지만 전체적으로 보면, '구표면'처럼 매우 다루기 쉽지 않은 공간이다. 이러한 2차원 공간들 이외에도, 더 높은 차원의 공간들이 다양한 모양으로 존재한다. 또한 각 공간마다 여러가지 좌표계를 사용할 수 있다.어떤 공간에 존재하는 물리량(physical quantity)은 어떤 좌표계를 설정하던 같아야 한다 (좌표계와 독립적이여야만 한다). 하지만 그 물리량을 포함하고 있는 공간과는 독립적이지 않아도 된다. 예를 들어 설명하면, 평면(유클리드 2차원 공간)에서 모든 삼각형은 내각의 합이 180도이다. 하지만 '구표면'에서는 아니다. 즉 공간(space)이 달라지면, 물리량도 달라진다. 하지만 같은 공간에서 좌표계가 달라진다고 물리량이 달라지지 않는다는 것이다.
이제 좌표계에 대해 좀 더 자세히 살펴보자. 다시 유클리드 공간으로 돌아와서, 아래 그림과 같은 2차원 직교 좌표계(Cartesian)를 보자. 아까 말했듯, 우리가 여태껏 주로 다뤄왔던 좌표계이며, 서로 수직인 x축과 y축으로 이루어져있다. 이 두 축은 하나의 교점을 가지며, 이 점을 원점(origin)이라고 부른다.
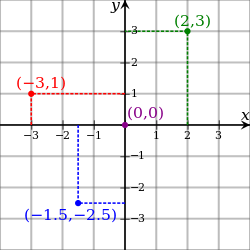
이 두 축은 또한 하나의(unique) 평면을 만드는데, 바로 x y 평면이다. 이러한 평면을 수학용어로는 'coordinate surface'라고 부른다. 이 평면 상에 있는 모든 점은 x와 y의 값으로 나타내질 수 있다. 사실 이는 매우 당연한 말이다. 이런 자명한 사실을 수학자들이 좋아하는 어려운 '정의'로 표현해보자.
1. n차원 카테시안 좌표계에서는 n개의 수직한 축(axis)이 존재한다.
2. n개의 축 모두 서로와 수직(mutually orthogonal)하며, 원점에서만 서로 만난다.
3. 이 축들로 인해 나뉘어지는 (n-1)! 개의 좌표 평면(coordinate plane)이 존재한다.
위의 정의는 '직교 좌표계'에서의 정의이다. 이제 이를 확장시켜(일반화) 모든 좌표계에 맞는 정의로 바꿔보자.
1. 좌표 축은 적어도 1번이상 서로 교차하는 선(곡선 or 직선)이며, 그 교점 중 하나는 원점(origin)으로 골라질 수 있다.
2. 좌표 축은 서로 수직이여야만 할 필요는 없다.
3. 2개의 좌표 축은 (곡면일 수도 있는) 특정한 coordinate surface를 만든다.
이렇게 만들어진 평면은 'product space(곱공간)'라고 부른다. 이러한 평면은 s = x*y 이런식으로 곱으로 표현할 수 있기 때문이다.이 product space에 대해 좀 더 자세히 알아보자. 위의 카테시안 좌표계를 살펴볼건데, n차원 좌표계는 머리속으로 상상하기 어려우므로, 상상이 가능한 2차원이나(xy) 3차원(xyz)으로 생각하면 된다. 예를 들어 쉽게 3차원이라고 하면, 어떤 축 1개가 다른 수직한 한 축을 따라서 쭉 움직인다고 생각해보자. 그 움직인 면적은 '평면'이 되며 이것이 'product space'이다. 이렇게 product space가 만들어지는 과정에서 좌표가 찍히게 되며, 이것이 '좌표계(coordinate system)'를 만드는 원리이다. 이제 어떤 3차원 공간에 있는 원과 한 접선을 생각해보자. 접선이므로 당연히 원의 반지름과는 서로 수직하다. 더해서, 아래 그림처럼 원의 면 방향과도 수직이다.
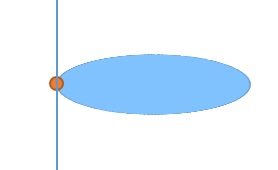
이때 머리속으로 이 원을 접선을 따라서 쭉 움직여보자. (접선을 둘러 원을 회전시키는 것이 아니라, 위아래로) 이때 원이 움직인 면적은 '원기둥(cylinder)'가 된다. 즉 원과 직선의 product space는 원기둥인 것이다. 여기서도 이 원기둥 안의 어떤 점은, 원과 직선의 값을 이용해 좌표로 찍히게 된다. 위의 예제는 유클리드 3차원 공간에서, 직교 좌표계가 아닌 다른 좌표계를 만드는 원리이다. 우리가 만든 것들은 그 중 가장 대표적인 '원통 좌표계'이다.
마지막으로 임의의 2개의 곡선을 생각해보자. 마찬가지 방법으로 product space를 만들어 좌표계를 만들 수 있다. 즉 '비유클리드 공간'에서도 가능한 것이다. 꽤나 복잡하지만 말이다. 이렇게 만들어진 좌표계를 일반 좌표계 (generalized coordinate system)라고 한다. 2개의 곡선을 사용했다는 점을 상기한 채로 아래 그림을 보자.
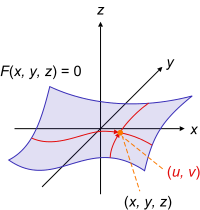
위의 그림을 보면 3차원 공간에서 어떠한 점을 표시할 때, 검정색은 직교 좌표계(데카르트 좌표계)를 이용해 (x, y, z) 총 3개의 항으로 표현한 것이며, 빨간색은 임의의 일반 좌표계를 이용해 (u, v) 총 2개의 항으로 표현한 것이다. 그림을 잘 보면 2개의 빨간색 곡선이 있음을 알 수 있다.
'그래픽스 > 수학 물리' 카테고리의 다른 글
| 제곱근과 실수 (0) | 2024.08.27 |
|---|---|
| 실수, 유리수, 무리수, 정수, 자연수, 순환소수, 비순환소수란? (0) | 2024.08.27 |
| 동차 좌표계란? (0) | 2024.05.02 |
| 투영 행렬 유도와 ndc (0) | 2024.05.02 |
| 지수의 밑변환 공식, 로그의 밑변환 공식 - 개념, 유도, 적용 (0) | 2024.04.24 |
