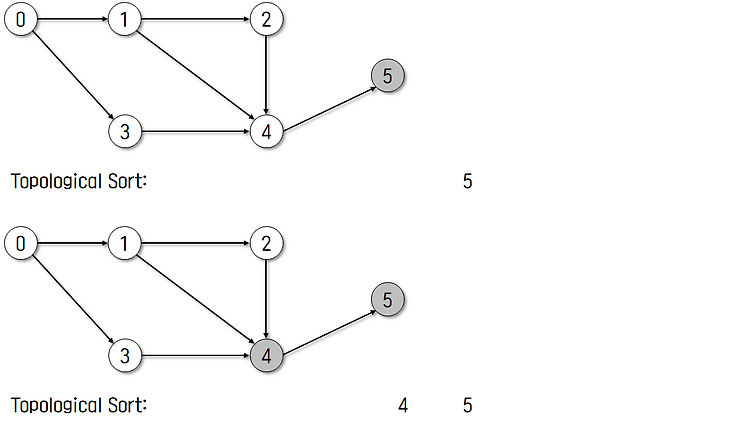
DAG에 대한 토폴로지 정렬 알고리즘
위상 정렬이란 방향이 있는 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점들을 나열하는 것이다. 싸이클이 없는(DAG, Directed Acyclic Graph) 그래프에선 가능하며 하나의 유향 그래프에서 여러 위상 정렬이 가능하다.
시간 복잡도 : O(V + E) / V (Vertex) : 노드, E (Edge) : 간선 => Best Case, Worst Case 동일.
DFS와 관련된 다양한 유형의 에지의 출발 시간 사이의 관계이다.
Tree edge (u, v): departure[u] > departure[v]
Back edge (u, v): departure[u] < departure[v]
Forward edge (u, v): departure[u] > departure[v]
Cross edge (u, v): departure[u] > departure[v]DAG에는 백 에지가 없다.. 따라서 출발 시간이 감소하는 순서로 정점을 정렬하면 그래프의 토폴로지 순서(왼쪽에서 오른쪽으로 가는 모든 모서리).

Kahn의 위상 정렬 알고리즘 DFS

7 5 3 1 4 2 0 6
7 5 1 2 3 4 0 6
5 7 3 1 0 2 6 4
3 5 7 0 1 2 6 4
5 7 3 0 1 4 6 2
7 5 1 3 4 0 6 2
5 7 1 2 3 0 6 4
3 7 0 5 1 4 2 6
… 등등
모든 방향 모서리에 대해 u —> v, u 전에 온다 v 주문에. 예를 들어, 토폴로지 순서의 그림 표현 [7, 5, 3, 1, 4, 2, 0, 6] 이다:

칸-알고리즘(그래프)
L —> 정렬된 요소를 포함할 빈 목록
S —> 들어오는 가장자리가 없는 모든 정점의 집합(즉, 차수가 0임)
S가 비어 있지 않은 동안 do
S에서 꼭짓점 n 제거
L의 꼬리에 n을 더하다
n에서 m까지의 모서리 e가 있는 각 정점 m에 대해
그래프에서 간선 e 제거
m에 다른 들어오는 가장자리가 없으면 m을 S에 삽입한다.
m을 S에 삽입
그래프에 모서리가 있는 경우
반환 보고서 "그래프에 하나 이상의 주기가 있다."
또 다른
반환 L "위상적으로 정렬된 순서"아래는 개인 코드, 재해석했다.
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <map>
#define y first // 시작하는 지점
#define x second // 향하는 지점
using namespace std;
using IntVector = vector<int>;
IntVector Graph[100];
IntVector InDegree, Res;
int GraphSize = 0;
// DFS를 사용한 방법
void TopologicalSort()
{
stack<int> s;
for (int i = 0; i < GraphSize; i++)
{
// 연결 되어있는 노드가 존재하지 않을 시
if (InDegree[i] == 0)
{
s.push(i);
}
}
while (!s.empty())
{
int val = s.top(); s.pop();
Res.push_back(val);
for (auto node : Graph[val])
{
if (--InDegree[node] == 0)
s.push(node);
}
}
// 그래프에 에지가 있는 경우 그래프에는 적어도 하나의 사이클이 있다.
for (int i = 0; i < GraphSize; i++)
{
if (InDegree[i] > 0)
{
Res.clear();
return;
}
}
}
int main()
{
// 위의 다이어그램에 따라 그래프 가장자리의 Vector
vector<pair<int,int>> edges
{
{ 0, 6 }, { 1, 2 }, { 1, 4 }, { 1, 6 }, { 3, 0 }, { 3, 4 },
{ 5, 1 }, { 7, 0 }, { 7, 1 }
};
GraphSize = edges.size() - 1;
InDegree.resize(GraphSize);
// 그래프 구성
for (auto node : edges)
{
Graph[node.y].push_back(node.x);
InDegree[node.x]++;
}
TopologicalSort();
if (!Res.empty())
{
for (int val : Res)
cout << val << " ";
}
else
cout << "그래프가 하나의 사이클이 존재하므로 위상 정렬 불가능";
return 0;
}결과
7 5 1 2 3 4 0 6출처 : https://www.techiedelight.com/ko/topological-sorting-dag/
출처 : https://www.techiedelight.com/ko/kahn-topological-sort-algorithm/
'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| BSP(Binary Space Partitioning)알고리즘을 응용해 로그라이크류 게임 방만들기 (0) | 2022.09.17 |
|---|---|
| 시간 복잡도에 따른 알고리즘 목록 (0) | 2022.08.31 |
| 분리 집합 (Disjoint Set) / Union-Find (0) | 2022.08.14 |
| 최소 스패닝 트리 (MST) / 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2022.08.14 |
| 가중치 그래프와 임계 경로(Critical Path) (0) | 2022.08.14 |