이진 공간 분할법(Binary Space Partitioning, BSP) 은 재귀적으로 유클리드 공간을 초평면 상의 볼록 집합으로 분할하는 기법이다. 분할 과정으로 BSP 트리라 불리는 트리 구조가 만들어진다.

doom은 3차원처럼 보이지만 실제로는 2차원이고 그 2차원을 나타내기 위해 사용됐다.
BSP알고리즘을 통한 로그라이크류 방만들기

0: 빈 공간 1 : 방, 3: 가로분할 길, 4: 세로분할 길
로그라이크 게임을 하다보면 일정한 맵을 돌려쓰는 게임도 있긴하지만 매번 새로운 맵을 생성하는 게임들이 존재한다. 매번 새로 맵을 생성할때 BSP알고리즘을 응용하여 새로 맵을 만들수 있다. 위에서 설명한 BSP알고리즘에서 둔각을 찾아 반복하여 나누는 방법이 아니라 2차원상에서 직사각형 모양으로만 방을 나눠 매번 새로운 맵을 생성하는 방법이다.
알고리즘
1. 방을 이분할한다.
분할비율은 4:6~6:4로할지에 대해서만 랜덤으로 설정하였다.
if(rLen/cLen>1 ||(cLen/rLen<=1 && rand()%2)){ //가로세로 랜덤 분할및 한쪽으로만 분할 막기
int divideNum = (r2-r1)*(rand() % 3 + 4)/10; // 랜덤비율설정
...
}2. 분할이 끝나면 방을 만든다.
분할된 공간을 1을 넣어 방으로 표시를 해준다. 나중에 길을 넣기위해서 전체 직사각형 면들을 각각 2씩 빼서 방을 만들어주었다.
if (depth ==0 || (r2 - r1 <= 10 || c2 - c1 <= 10)) {
for (int i = r1+2; i < r2-2; i++) {
for (int j = c1 + 2; j < c2 - 2; j++) {
Dungeon[i][j] = 1;
}
}
return {r1+2, c1+2, r2-3, c2-3, r1+2, c1+2, r2-3, c2-3 };
}3. 분할된 방사이에 길을 만들어 합친다.
재귀를 통해 길을 좀더 수월하게 만들기 위해서 왼쪽분할되는 방을 1,2 오른쪽 분할되는 방을3,4라고 했을때 2,3을 연결을 시켜주었다.
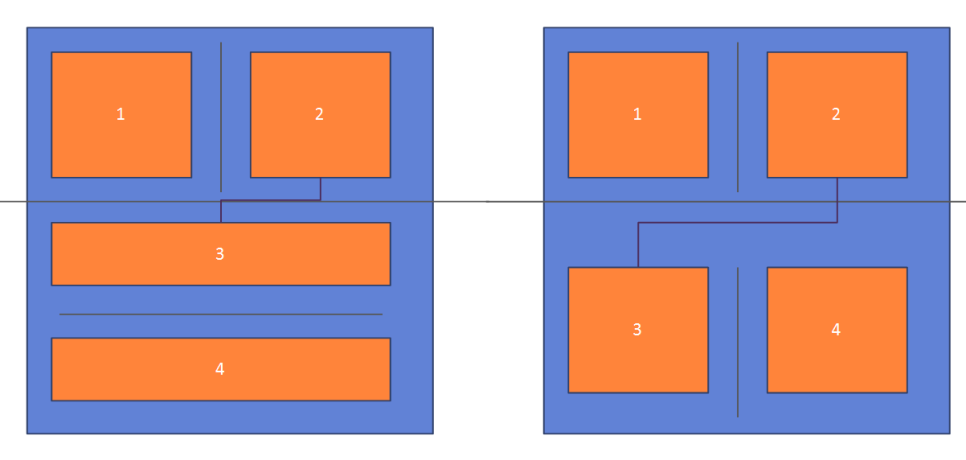
...
Dungeon[temp1.r4 + 1][(temp1.c3 + temp1.c4) / 2] = 4;
Dungeon[temp1.r4 + 2][(temp1.c3 + temp1.c4) / 2] = 4;
Dungeon[temp2.r1 - 1][(temp2.c1 + temp2.c2) / 2] = 4;
Dungeon[temp2.r1 - 2][(temp2.c1 + temp2.c2) / 2] = 4;
int rmin = min((temp1.c3 + temp1.c4) / 2,(temp2.c1 + temp2.c2) / 2);
int rmax = max((temp1.c3 + temp1.c4) / 2, (temp2.c1 + temp2.c2) / 2);
for (int i = rmin; i <= rmax; i++) {
Dungeon[temp2.r1 - 2][i] = 4;
}
...#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string>
#include<string.h>
#include<math.h>
using namespace std;
#define DungeonSize 60
int Dungeon[DungeonSize][DungeonSize];
//1.분할한다.
//2. 분할이 끝나면 방을 만든다.
//3. 방을 연결한다.
typedef struct DungeonLocation{
int r1, c1, r2, c2;
int r3, c3, r4, c4;
};
DungeonLocation divideDungeon(int depth, int r1, int c1, int r2, int c2) {
DungeonLocation Location;
//2. 방을 만든다.
if (depth ==0 || (r2 - r1 <= 10 || c2 - c1 <= 10)) {
for (int i = r1+2; i < r2-2; i++) {
for (int j = c1 + 2; j < c2 - 2; j++) {
Dungeon[i][j] = 1;
}
}
return {r1+2, c1+2, r2-3, c2-3, r1+2, c1+2, r2-3, c2-3 };
}
//1. 분할한다
//3. 방을 합친다.
int rLen = r2 - r1;
int cLen = c2 - c1;
DungeonLocation temp1, temp2;
if(rLen/cLen>1 ||(cLen/rLen<=1 && rand()%2)){ // 세로분할
int divideNum = (r2-r1)*(rand() % 3 + 4)/10;
//방 분할
temp1 = divideDungeon(depth - 1, r1, c1, r1+divideNum, c2);
temp2 = divideDungeon(depth - 1, r1 + divideNum, c1, r2, c2);
//방합치기.
Dungeon[temp1.r4 + 1][(temp1.c3 + temp1.c4) / 2] = 4;
Dungeon[temp1.r4 + 2][(temp1.c3 + temp1.c4) / 2] = 4;
Dungeon[temp2.r1 - 1][(temp2.c1 + temp2.c2) / 2] = 4;
Dungeon[temp2.r1 - 2][(temp2.c1 + temp2.c2) / 2] = 4;
int rmin = min((temp1.c3 + temp1.c4) / 2,(temp2.c1 + temp2.c2) / 2);
int rmax = max((temp1.c3 + temp1.c4) / 2, (temp2.c1 + temp2.c2) / 2);
for (int i = rmin; i <= rmax; i++) {
Dungeon[temp2.r1 - 2][i] = 4;
}
}
else {// 가로분할
int divideNum = (c2 - c1) * (rand() % 3 + 4) / 10;
//방분할
temp1 = divideDungeon(depth - 1, r1, c1, r2, c1 + divideNum);
temp2 = divideDungeon(depth - 1, r1, c1 + +divideNum, r2, c2);
//방합치기
Dungeon[(temp1.r3 + temp1.r4) / 2][temp1.c4 +1] = 3;
Dungeon[(temp1.r3 + temp1.r4) / 2][temp1.c4 + 2] = 3;
Dungeon[(temp2.r1 + temp2.r2) / 2][temp2.c1 - 1] = 3;
Dungeon[(temp2.r1 + temp2.r2) / 2][temp2.c1 - 2] = 3;
int rmin = min((temp1.r3 + temp1.r4) / 2, (temp2.r1 + temp2.r2) / 2);
int rmax = max((temp1.r3 + temp1.r4) / 2, (temp2.r1 + temp2.r2) / 2);
for (int i = rmin; i <= rmax; i++) {
Dungeon[i][temp2.c1-2] = 3;
}
}
Location.r1 = temp1.r1, Location.r2 = temp1.r2, Location.c1 = temp1.c1, Location.c2 = temp1.c2;
Location.r3 = temp2.r3, Location.r4 = temp2.r4, Location.c3 = temp2.c3, Location.c4 = temp2.c4;
return Location;
}
void createDungeon() {
memset(Dungeon, 0, sizeof(Dungeon));
divideDungeon(5, 0, 0, DungeonSize, DungeonSize);
}
void printDungeon() {
for (int i = 0; i < DungeonSize; i++) {
for (int j = 0; j < DungeonSize; j++) {
printf("%d", Dungeon[i][j]);
}
printf("\n");
}
}
int main(void) {
createDungeon();
printDungeon();
}
'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence (0) | 2022.11.17 |
|---|---|
| 해시 함수의 종류 (0) | 2022.10.31 |
| 시간 복잡도에 따른 알고리즘 목록 (0) | 2022.08.31 |
| 유향 비순환 그래프 (DAG = Directed acyclic graph) 와 Khan 알고리즘을 이용한 위상 정렬 (Topological Sort) (0) | 2022.08.19 |
| 분리 집합 (Disjoint Set) / Union-Find (0) | 2022.08.14 |
