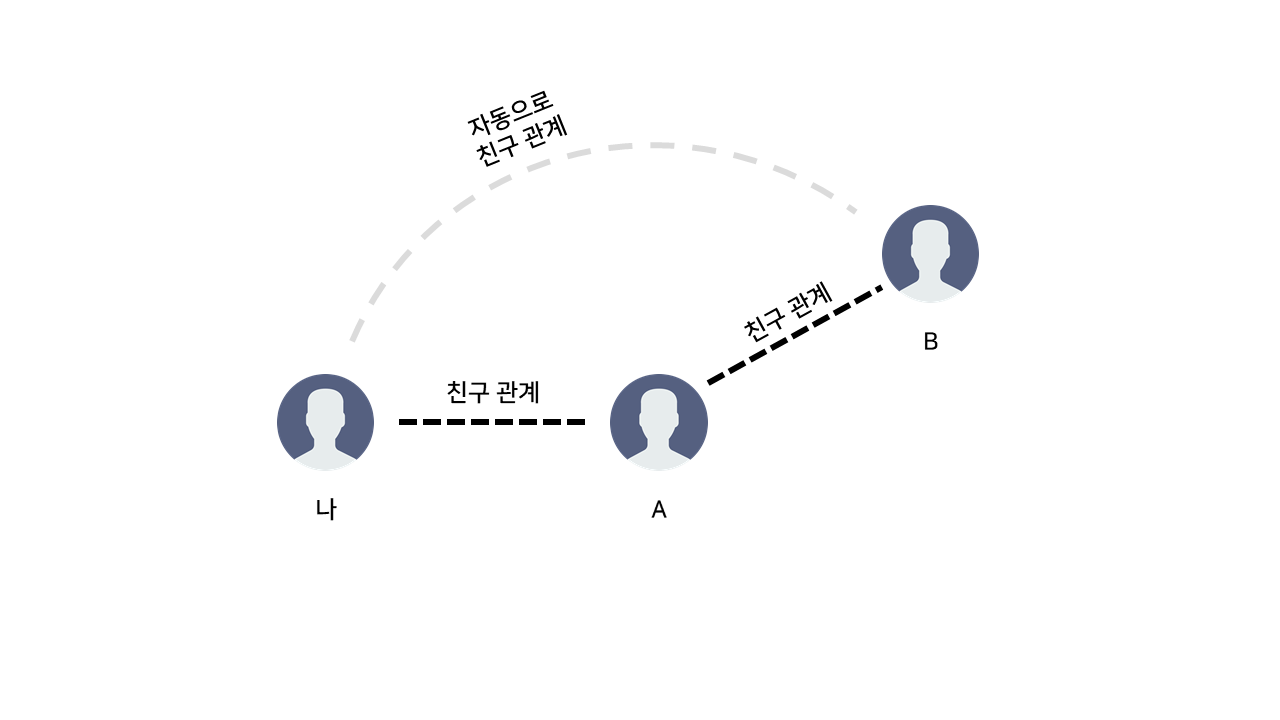
다음과 같은 메신저 프로그램이 있다. "A와 B가 친구 관계이고, 내가 A와 친구 관계이면 자동으로 나와 B는 친구 관계가 된다."
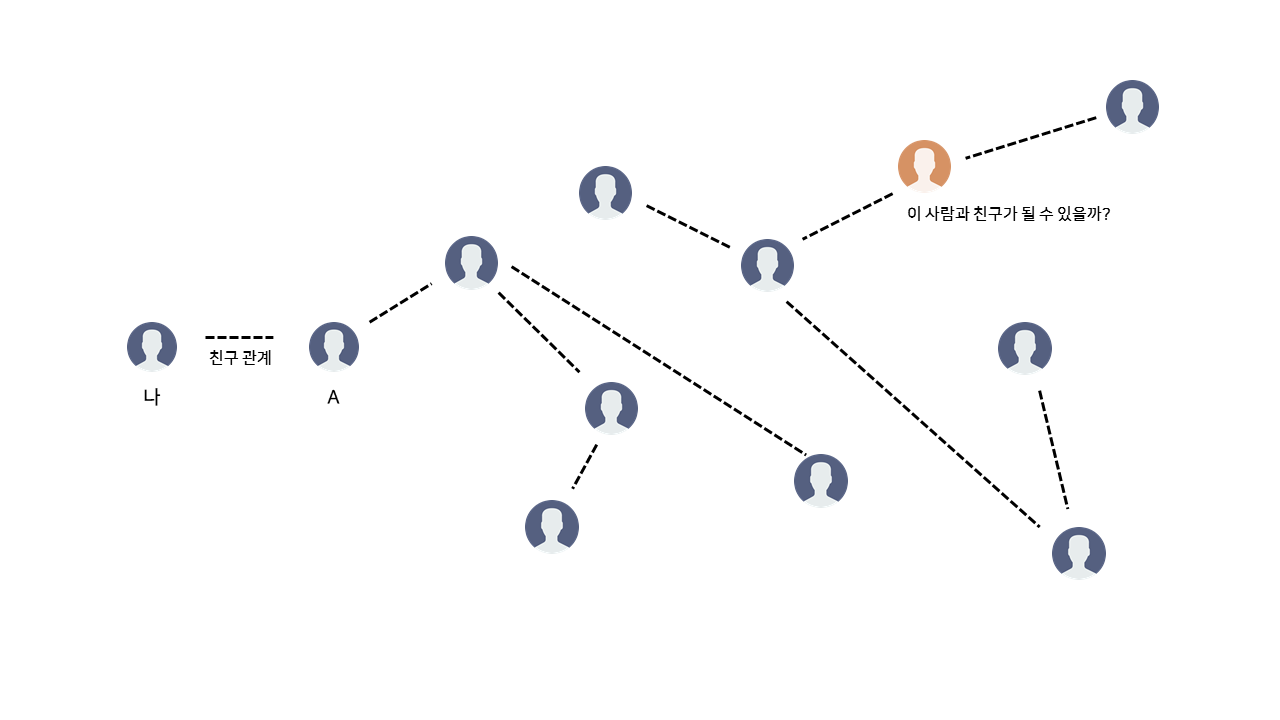
이 메신저 프로그램을 통해 내가 A라는 사람과 친구 관계를 맺었다. 다음과 같은 관계도에서, 내가 주황색으로 표시된 사람과 친구 관계가 될 수 있을지는 어떻게 알 수 있을까?
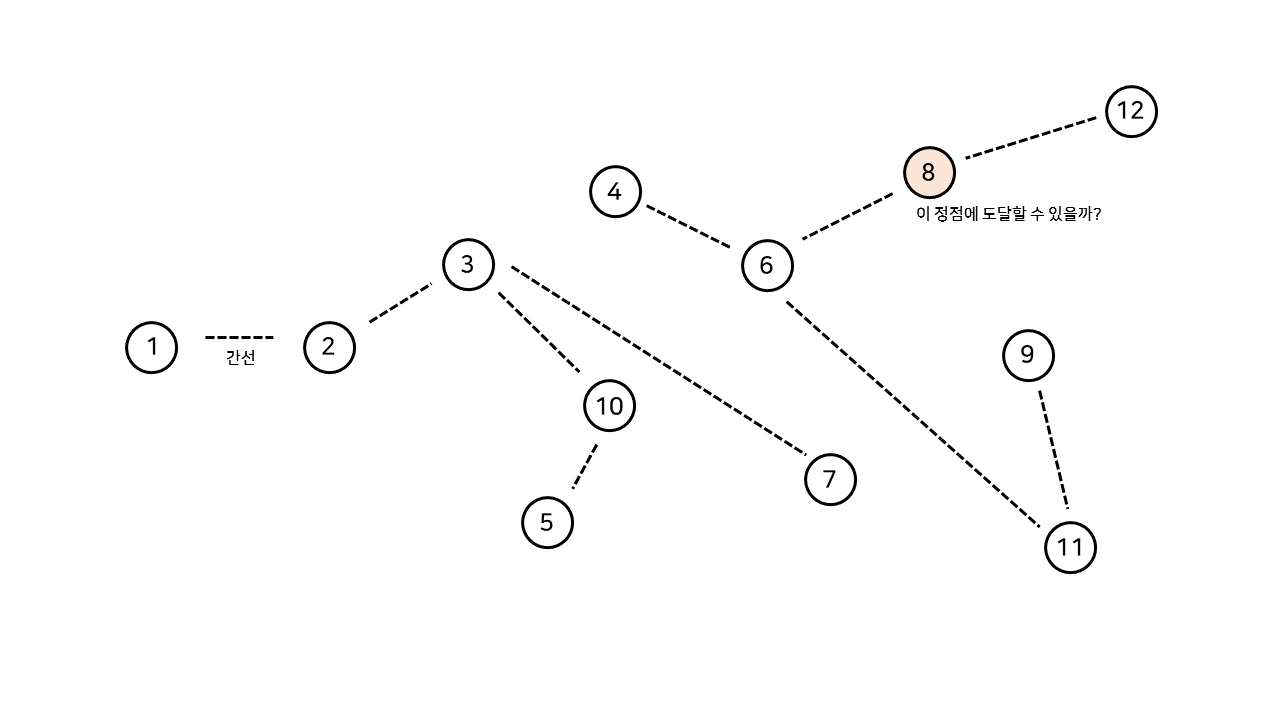
위처럼 친구 관계를 그래프로 나타낸 후 나를 시작으로 그래프 탐색(DFS, BFS)을 통해 목표 정점까지 도달할 수 있는지 확인하면 간단할 것이다. 하지만 새로운 친구 관계는 언제나 생겨날 수 있다.
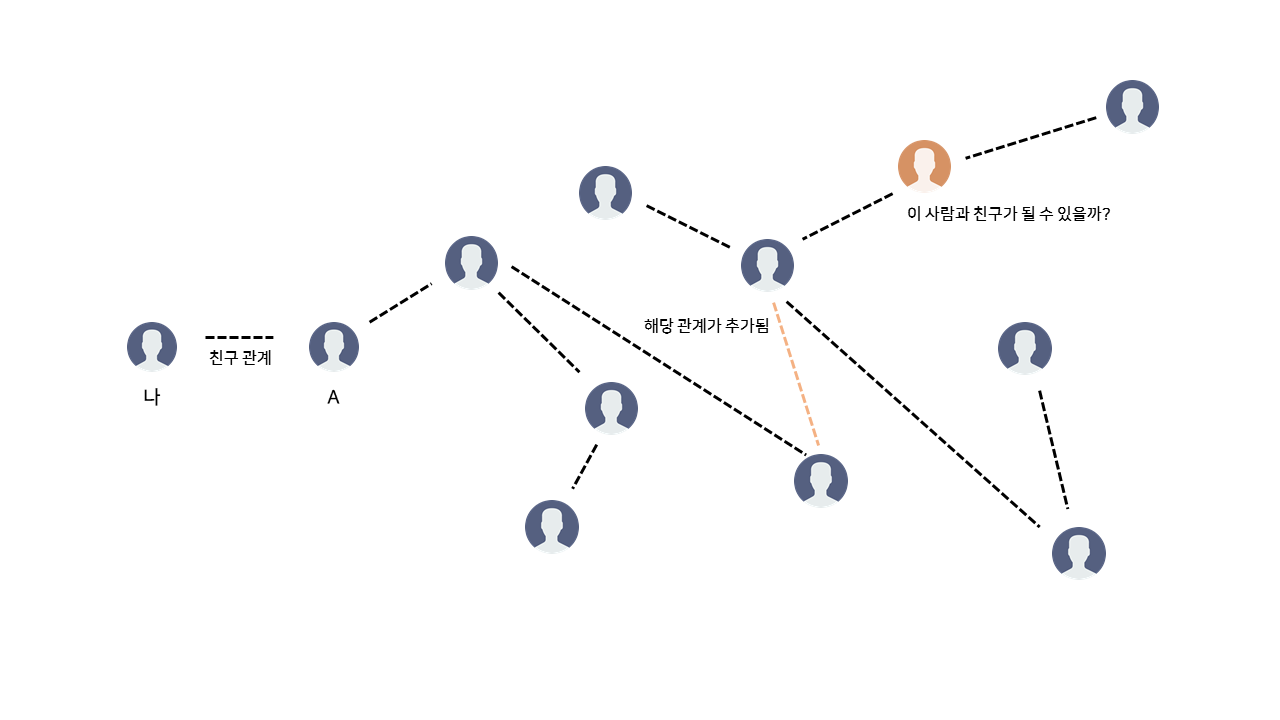
만약 주황색으로 표시된 친구 관계가 새로 생겼다고 할 때, 우리는 주황색 사람과 친구 관계가 될 수 있는지 알기 위해서다시 그래프 탐색을 진행해야 한다. 하지만 이 메신저 프로그램을 사용하는 사용자의 수가 어마어마하게 많다면, 새로운 친구 관계가 생겨날 때마다 그래프 탐색이 모든 사용자마다 진행되어야 하므로 매우 많은 시간이 걸릴 것이다.
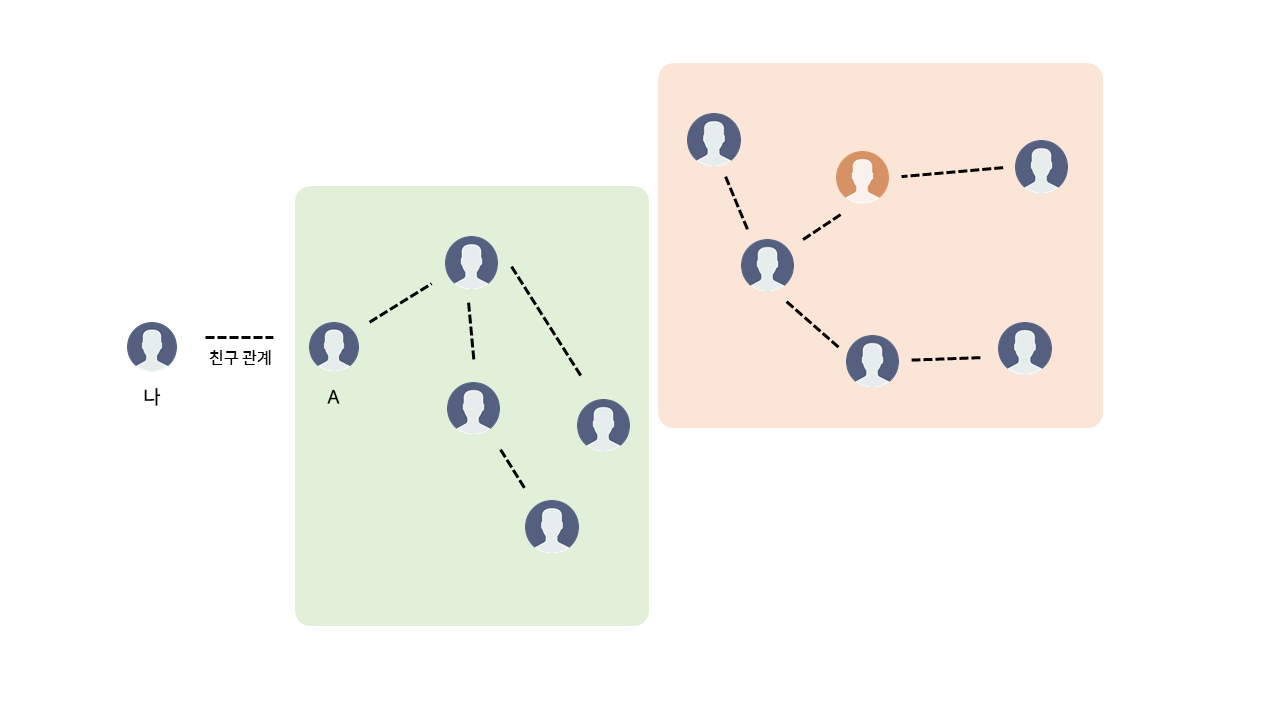
우리가 친구 관계를 그래프의 형태가 아닌, 그 사람이 속해 있는 그룹을 통해 표현한다면 소요되는 시간을 대폭 단축시킬 수 있을 것이다. 내가 A와 친구 관계를 맺었을 때, 나는 A와 같은 그룹에 속하게 된다. 이제 내가 다른 사용자와 친구 관계인지는 속한 그룹만 비교하면 되는 것이다. 위 그림에서 A가 속한 그룹을 'Green' 그룹이라 하고, 주황색으로 표시된 사람의 그룹을 'Orange' 그룹이라 할 때, 나와 그룹이 다르므로 그 사람은 친구 관계가 아니라는 것을 쉽게 알 수 있다.
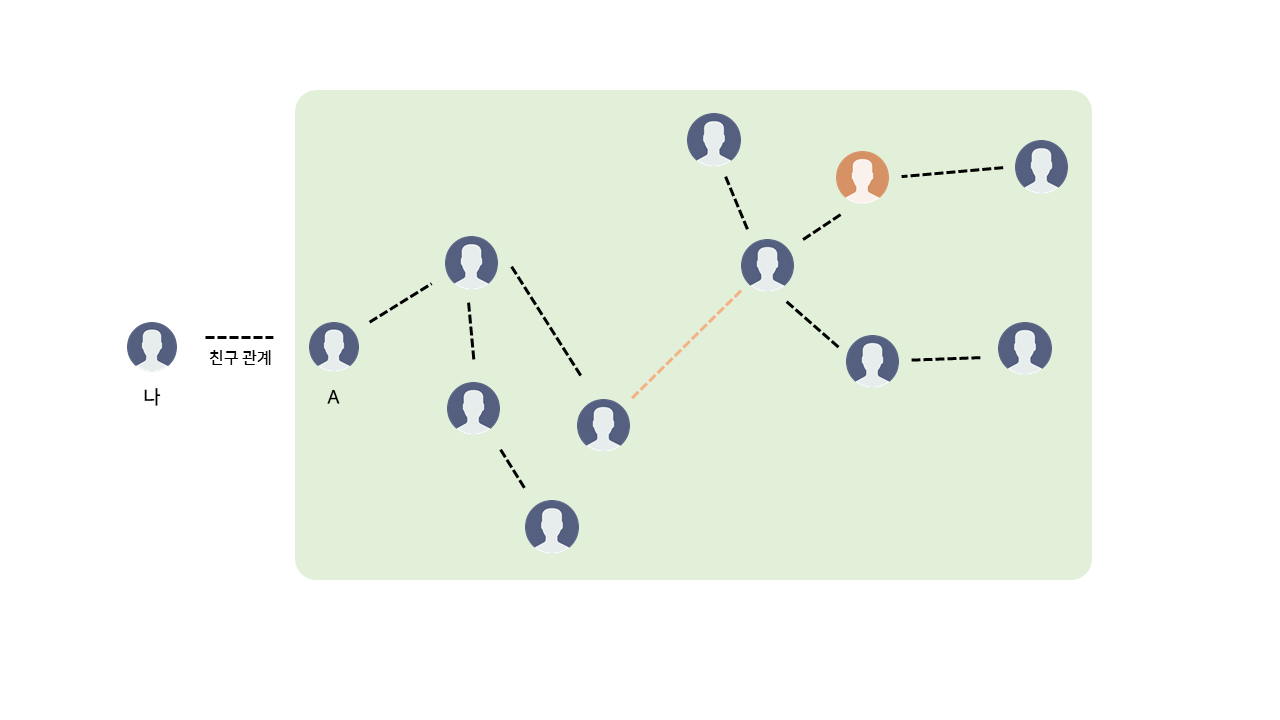
또한 위의 주황색 점선으로 표시된 새 친구 관계가 생성될 경우, 두 그룹을 합침으로써 친구 관계를 갱신할 수 있다.
이제 주황색으로 표시된 사람의 그룹도 'Green'이 되었으므로, 나와 같은 그룹임을 통해 친구 관계임을 알 수 있다.
분리 집합 (Disjoint Set)
분리 집합은 서로소 집합이라고도 한다. 용어의 의미처럼 분리 집합은 다음과 같은 특징을 가진다.
전체집합 U에 대해, U의 분리 집합 A, B는 다음 조건을 만족한다.
- A, B는 U의 부분집합이다.
- A, B는 공통 원소를 가지지 않는다.
- A, B의 합집합이 곧 전체집합 U이다. (A, B에 속하지 않는 U의 원소가 없어야 한다.)
※ 이는 분리 집합의 개수가 3개 이상일 때도 동일하게 적용된다.
즉, 이미 존재하는 집합 U에 대해 겹치는 부분이 발생하지 않도록 모든 원소들을 분리한 부분집합을 말한다.
위의 메신저 프로그램 예시에서 나를 제외한 총 사용자 11명을 두 그룹으로 겹치지 않게 나눈 것과 같다.
Union-Find 알고리즘
Union-Find는 이러한 분리 집합을 구현하는 알고리즘으로, 각 그룹을 트리의 형태로 표현한다.
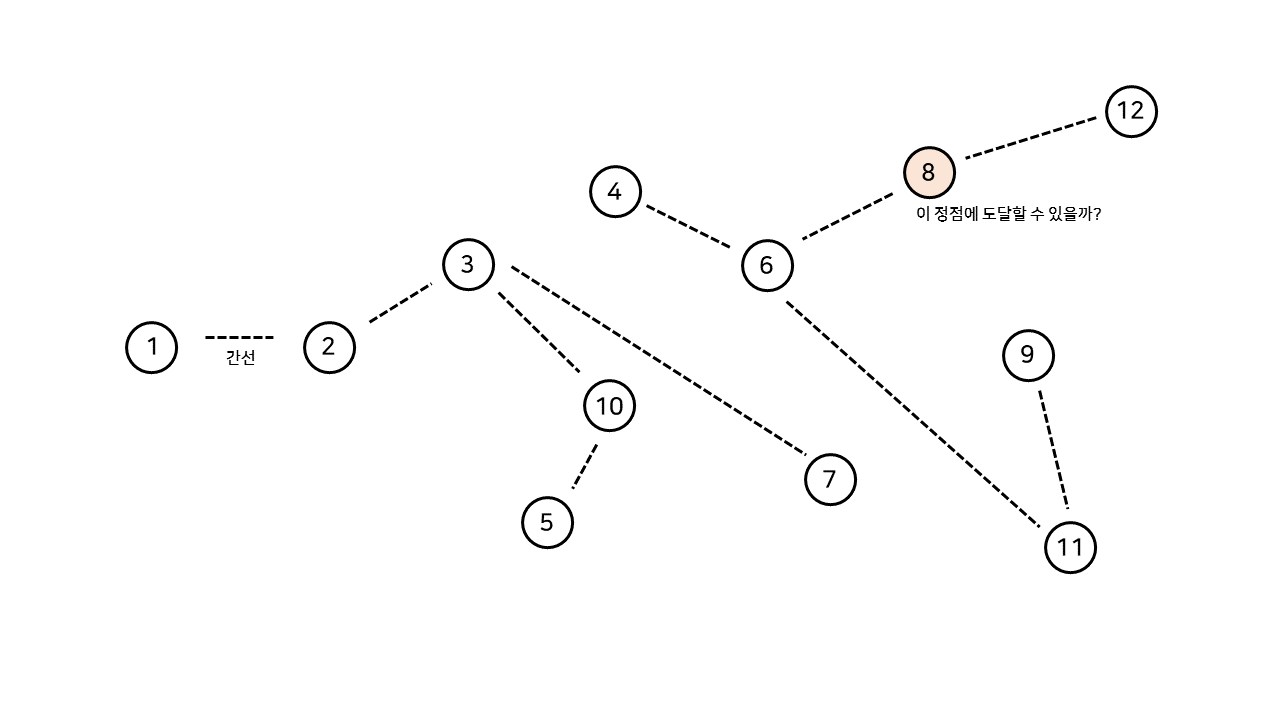
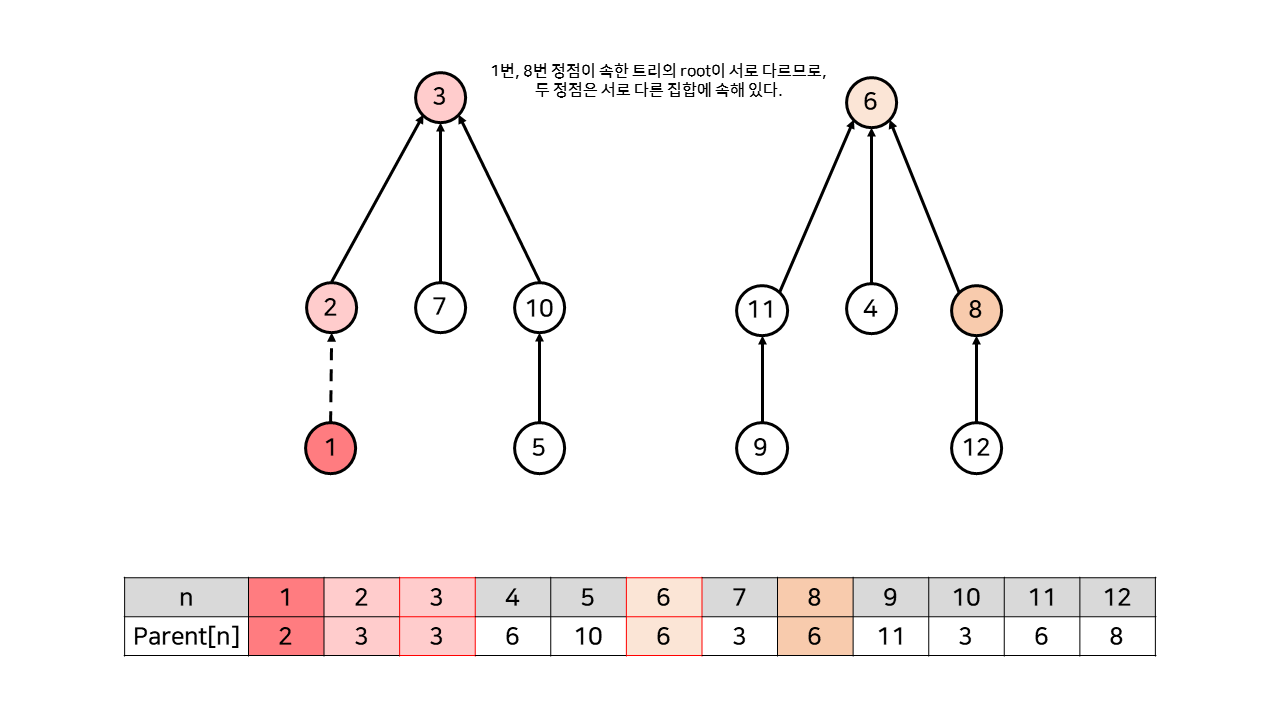
각 노드마다 그 노드의 부모 노드 번호를 기록하여, 그래프를 위처럼 트리 구조로 나타낸다. 이렇게 나타낸 트리는 항상 최상위 노드인 root 노드를 가지게 되는데, 바로 이 root 노드를 통해 그룹을 구별할 수 있게 된다. (root 노드의 경우, 부모 노드를 자기 자신으로 설정한다.) 1번 노드(나)와 2번 노드(A)가 친구 관계를 맺었으므로, 1번 노드를 2번 노드의 자식 노드로 연결한다. 만약 내가 8번 노드와 친구 관계임을 알고 싶다면, 내가 속한 트리의 root(3)와 8번 노드가 속한 트리의 root(6)을 비교하면 된다. 현재 상태에서는 root가 서로 다르므로, 친구 관계가 아니다.
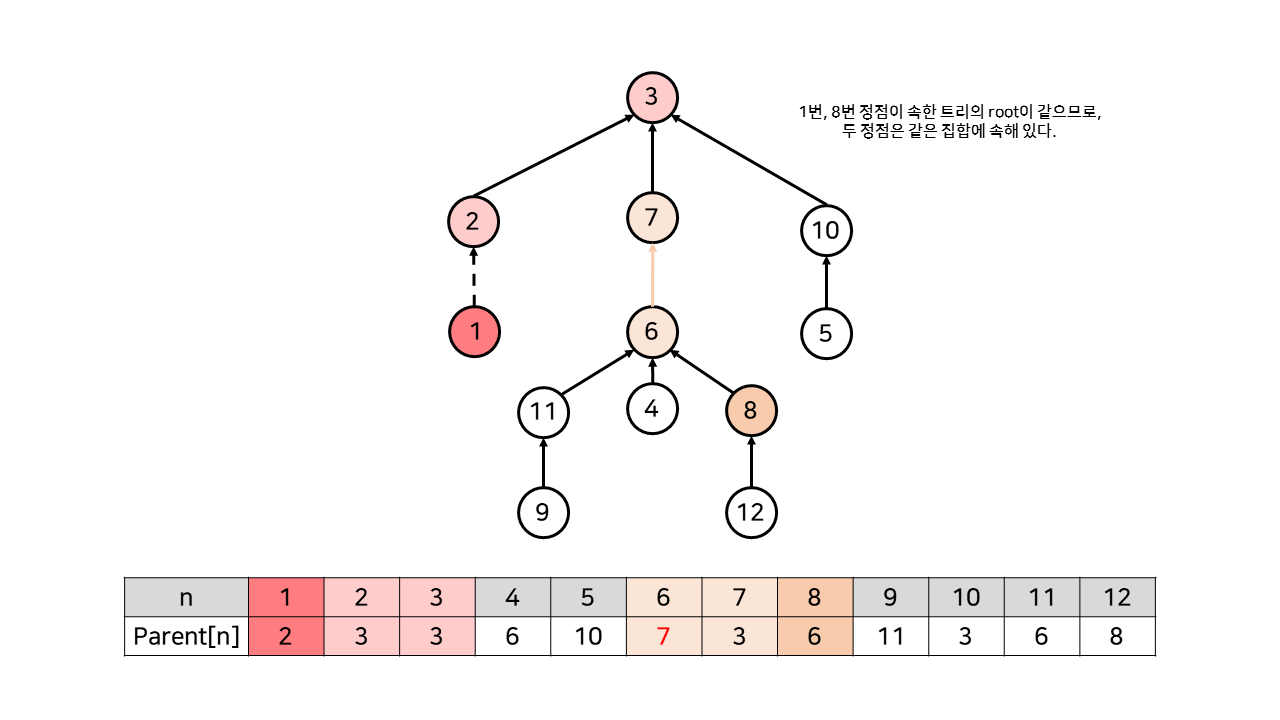
6, 7번 노드 간 친구 관계가 새로 만들어졌다면, 두 노드 중 하나의 부모 노드를 다른 하나로 지정하여 다음과 같이 트리를 병합할 수 있다. 그림에서 Parent[6]이 6에서 7로 갱신되었음을 알 수 있다. 이제 8번 노드의 root 노드도 3번이 되었으므로, 1번 노드와 8번 노드가 같은 그룹임을 알 수 있다. 따라서, 1번과 8번은 친구 관계이다.
지금까지 설명한 것을 구현하기 위해서는 다음과 같은 연산이 필요하다.
- root 노드를 찾는 작업 (Find)
- 두 트리를 병합하는 작업 (Union)
int find_root(int x) {
//x가 root이면, 그대로 반환한다.
if (x == parent[x]) return x;
//x가 자식 노드일 경우, 부모 노드에 대해 재귀실행한다.
return find_root(parent[x]);
}
void union_root(int x, int y) {
//x, y 정점의 최상위 정점을 각각 찾는다. (속한 트리의 루트 노드를 찾는다.)
x = find_root(x);
y = find_root(y);
if (x != y) {
//서로 다른 트리에 속한다면, 한 쪽의 트리를 다른 쪽에 붙인다.
parent[x] = y;
}
}최적화 : 경로 압축 (Path Compression)
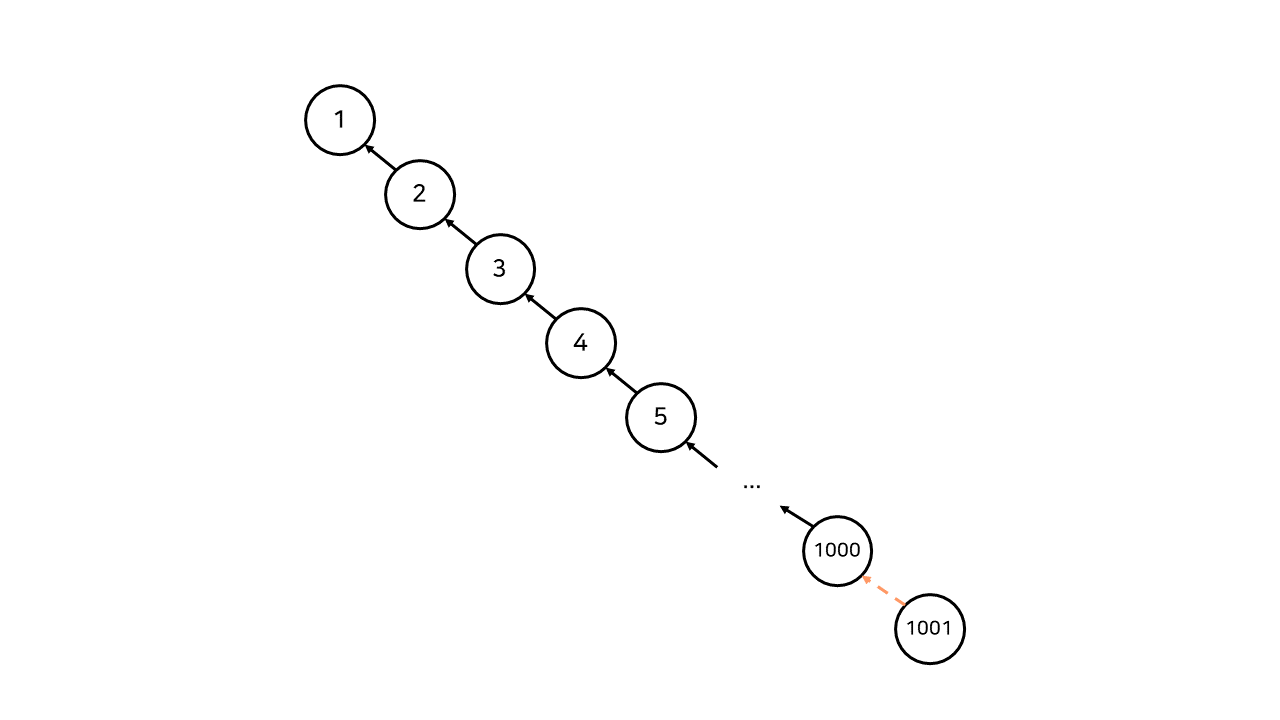
새로 생성되는 친구관계가 항상 (i, i + 1) 노드끼리 발생하는 상황을 가정해 보자. 1000명의 사용자가 위처럼 친구 관계를 맺었고, 이제 1001번 사용자가 1000번 사용자와 친구 관계를 맺으려 한다. 이 때, 1001번 사용자가 999번 사용자와 친구 관계임을 알기 위해선 root 노드를 찾아 비교하여야 하므로 항상 1번 노드까지 거슬러 올라가야 한다. 이는 시간적으로 매우 비효율적이다.
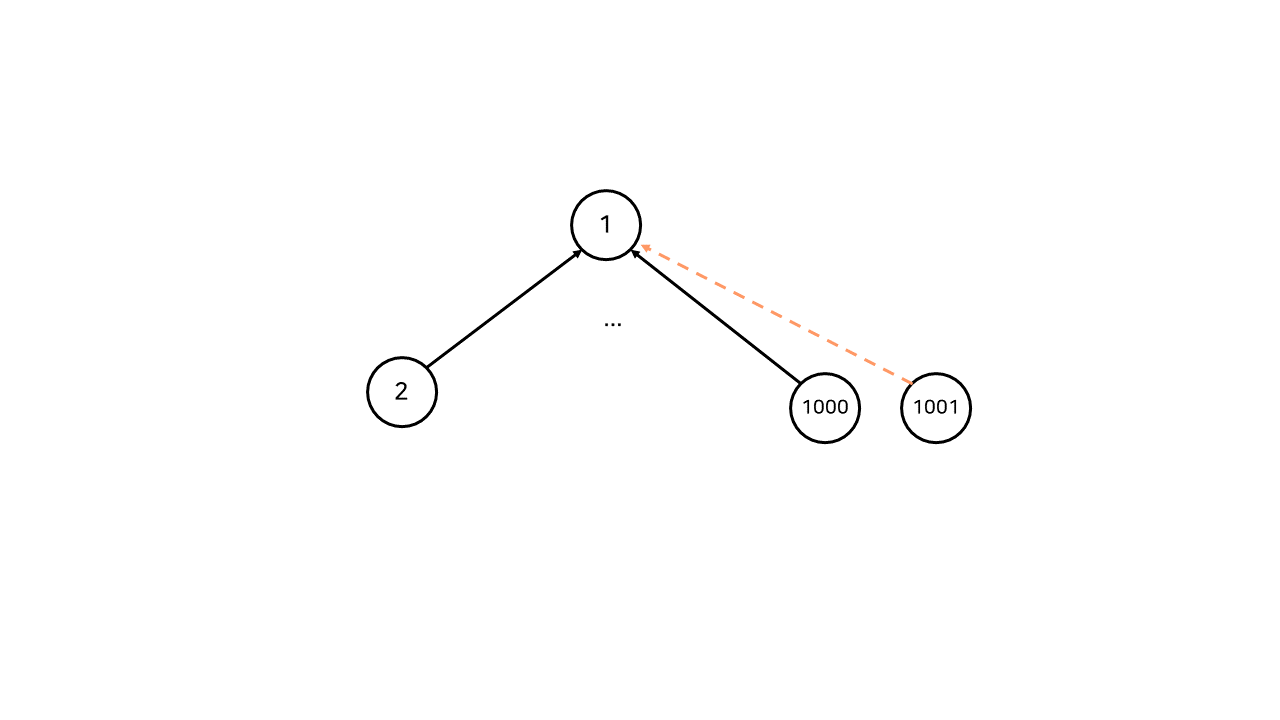
따라서 한 노드에 대해 Find 연산을 실행할 때마다 그 노드의 부모 노드를 항상 root 노드로 만들어준다면, 더 효율적으로 root 노드를 찾을 수 있을 것이다.
int find_root(int x) {
//x가 root이면, 그대로 반환한다.
if (x == parent[x]) return x;
//x가 자식 노드일 경우, 부모 노드에 대해 재귀실행한다.
//***이 때, parent[x]를 최종적으로 찾을 root 노드로 갱신한다.***
return parent[x] = find_root(parent[x]);
}최적화 : Union by Rank
결국 Find의 시간복잡도는 트리의 높이에 의해 결정된다.
따라서 Union 연산 시 항상 높이가 낮은 트리를 높은 트리에 붙임으로써 시간복잡도를 줄일 수 있다.
높이가 높은 트리가 낮은 트리에 붙을 경우, 합쳐진 트리의 높이가 더 많이 증가하기 때문이다.
※ node_rank[x] : x가 속한 트리의 높이
void union_root(int x, int y) {
//x, y 정점의 최상위 정점을 각각 찾는다. (속한 트리의 루트 노드를 찾는다.)
x = find_root(x);
y = find_root(y);
if (x != y) {
//서로 다른 트리에 속한다면, 한 쪽의 트리를 다른 쪽에 붙인다.
//***항상 높이가 낮은 트리를 높이가 높은 트리에 붙인다.***
if (node_rank[x] < node_rank[y]) parent[x] = y;
else parent[y] = x;
//만약 합친 두 트리의 높이가 같다면, 합친 후 트리의 높이를 1 증가시킨다.
if (node_rank[x] == node_rank[y]) {
parent[x] = y;
node_rank[x]++;
}
}
}'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| 시간 복잡도에 따른 알고리즘 목록 (0) | 2022.08.31 |
|---|---|
| 유향 비순환 그래프 (DAG = Directed acyclic graph) 와 Khan 알고리즘을 이용한 위상 정렬 (Topological Sort) (0) | 2022.08.19 |
| 최소 스패닝 트리 (MST) / 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2022.08.14 |
| 가중치 그래프와 임계 경로(Critical Path) (0) | 2022.08.14 |
| C++ vector empty()와 size()간 차이 (0) | 2022.08.04 |
