최소 스패닝 트리 (MST, Minimum Spanning Tree)
그래프의 스패닝 트리(신장 트리, Spanning Tree)란, 그래프의 모든 정점을 잇지만 사이클이 없는 부분 그래프를 의미한다.

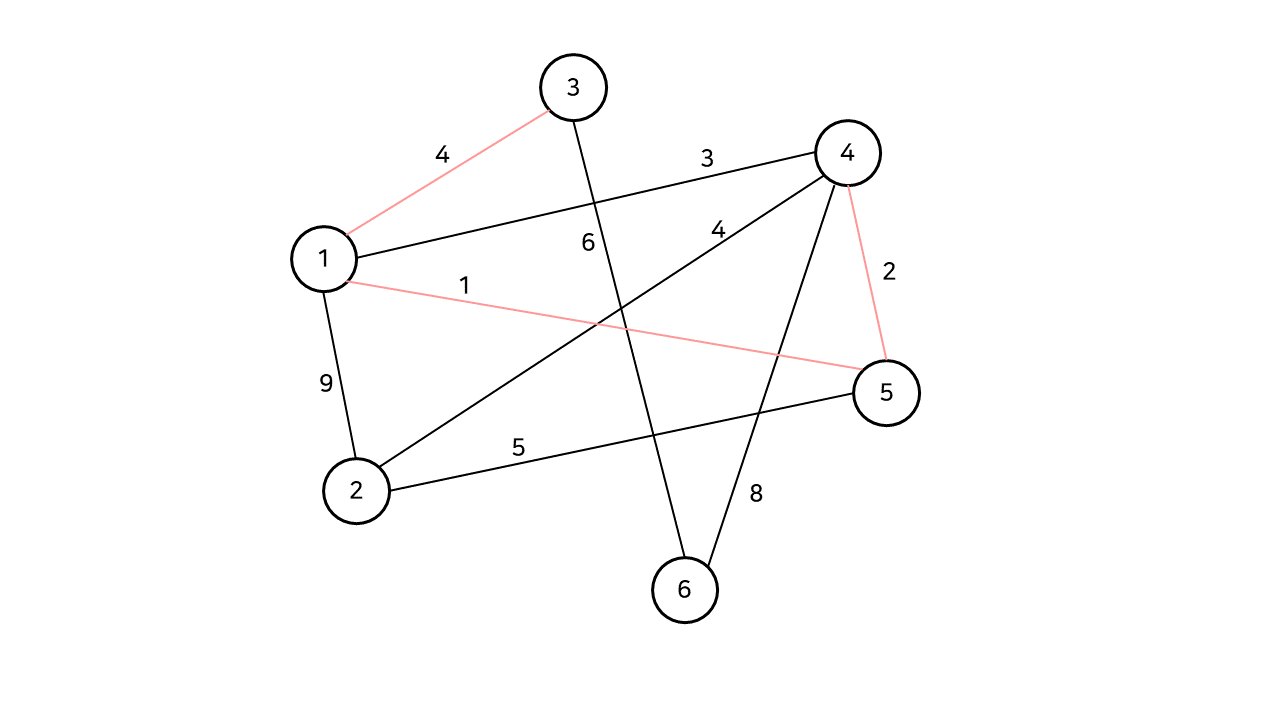
위와 같은 그래프에서, 양쪽의 붉은 간선으로 이어진 부분 그래프들은 모두 스패닝 트리에 해당한다. 즉, 형태와 관계없이 모든 정점을 사이클 없이 이을수만 있다면, 그것이 곧 스패닝 트리이다. 스패닝 트리는 이름처럼 트리의 일종이므로, V개의 모든 정점을 연결하는 간선의 수는 V - 1개이다.
최소 스패닝 트리(MST)는 이러한 스패닝 트리 중, 간선의 가중치 합이 최소가 되는 스패닝 트리를 말한다.

이러한 최소 스패닝 트리를 구하는 알고리즘은 대표적으로 Kruskal, Prim 알고리즘이 존재한다.
크루스칼 알고리즘 (Kruskal Algorithm)
크루스칼 알고리즘은 간선들을 중심으로, 그리디 알고리즘을 통해 최소 스패닝 트리를 구하는 알고리즘이다. 크루스칼 알고리즘의 동작 순서는 다음과 같다.
[동작 원리]
① 선택되지 않은 간선들 중 최소 가중치인 간선을 선택한다.
② 만약 그 간선을 선택했을 때, 지금까지 구성된 스패닝 트리에 사이클이 없을 경우에만 선택한다.
③ 총 V - 1(정점의 개수 - 1)개의 간선이 선택될 때까지 반복한다.
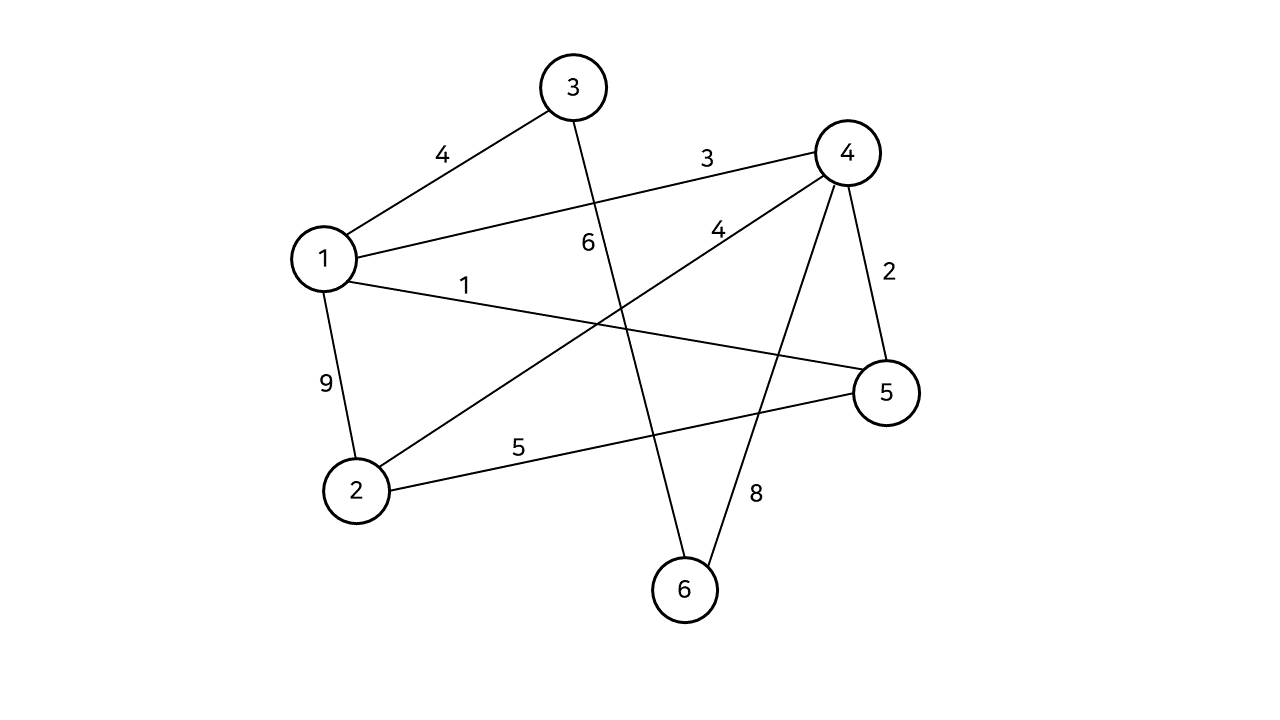
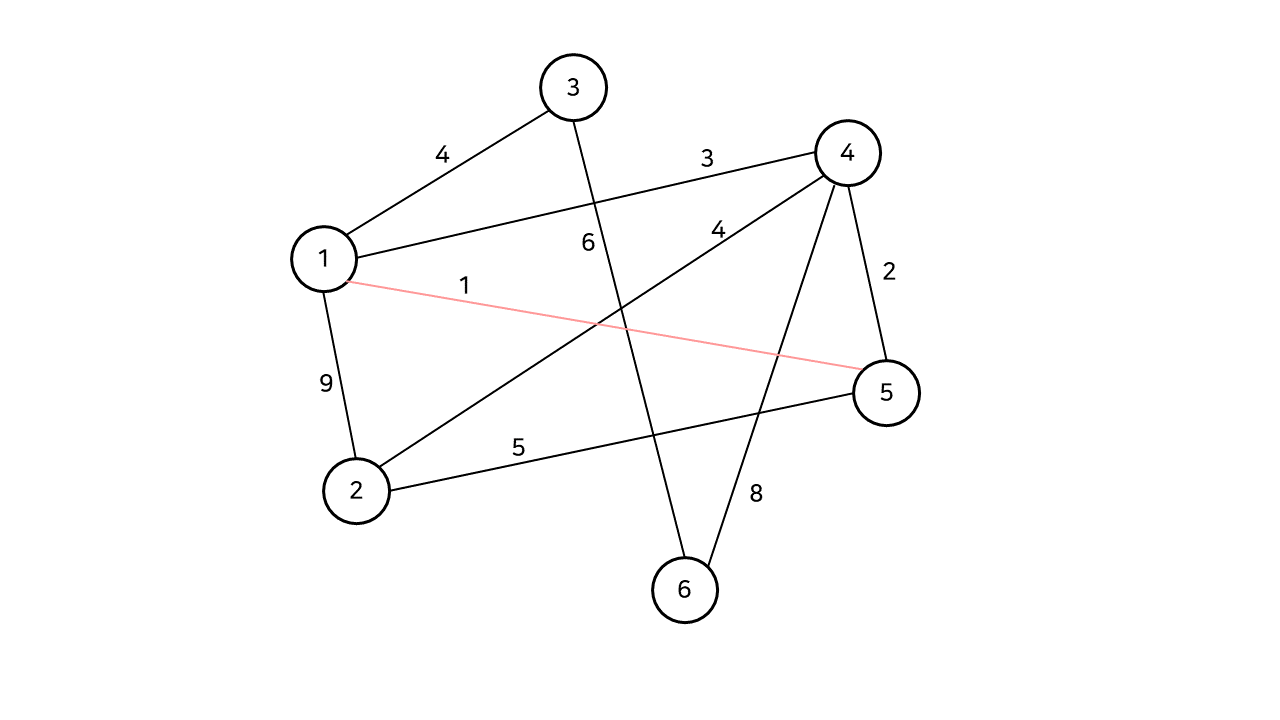
우선, 선택되지 않은 간선들 중 최소 가중치인 간선을 하나 선택한다. 이 경우에는 1, 5번 정점을 잇는 가중치 1인 간선이 선택된다. 이 간선을 선택해도 현재까지 구성한 스패닝 트리에 사이클이 발생하지 않으므로, 이를 스패닝 트리에 추가한다.
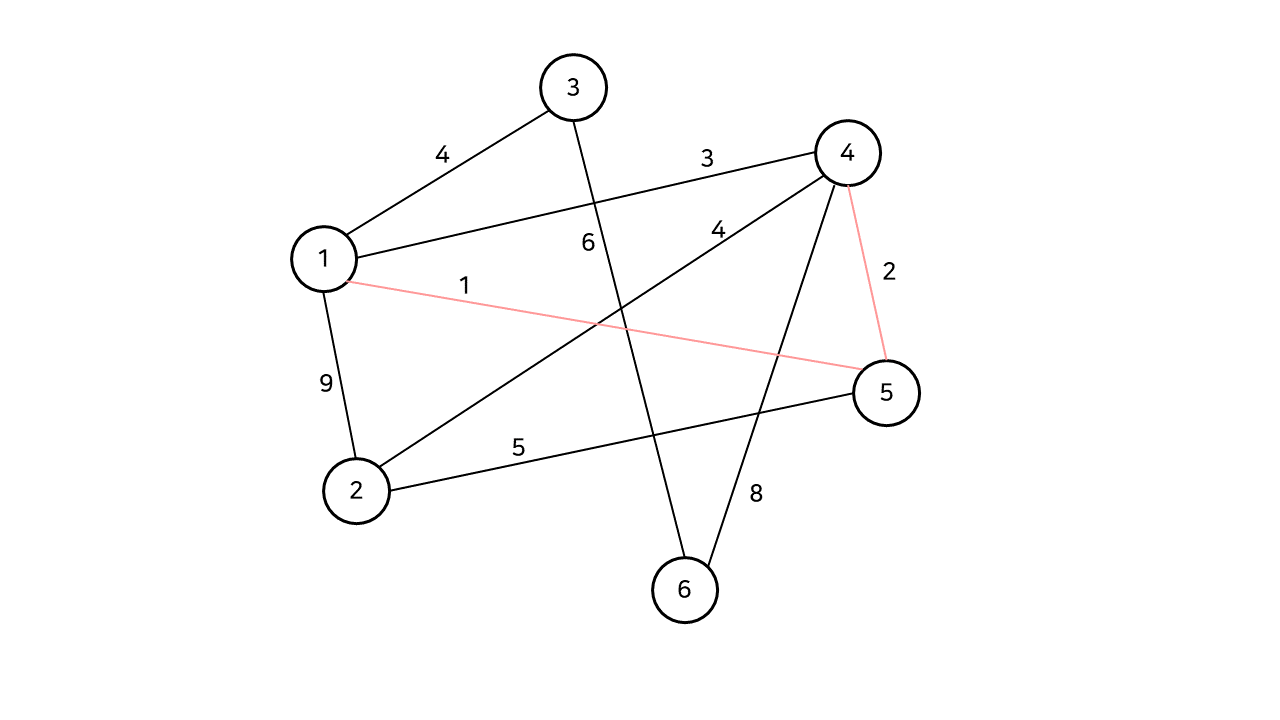
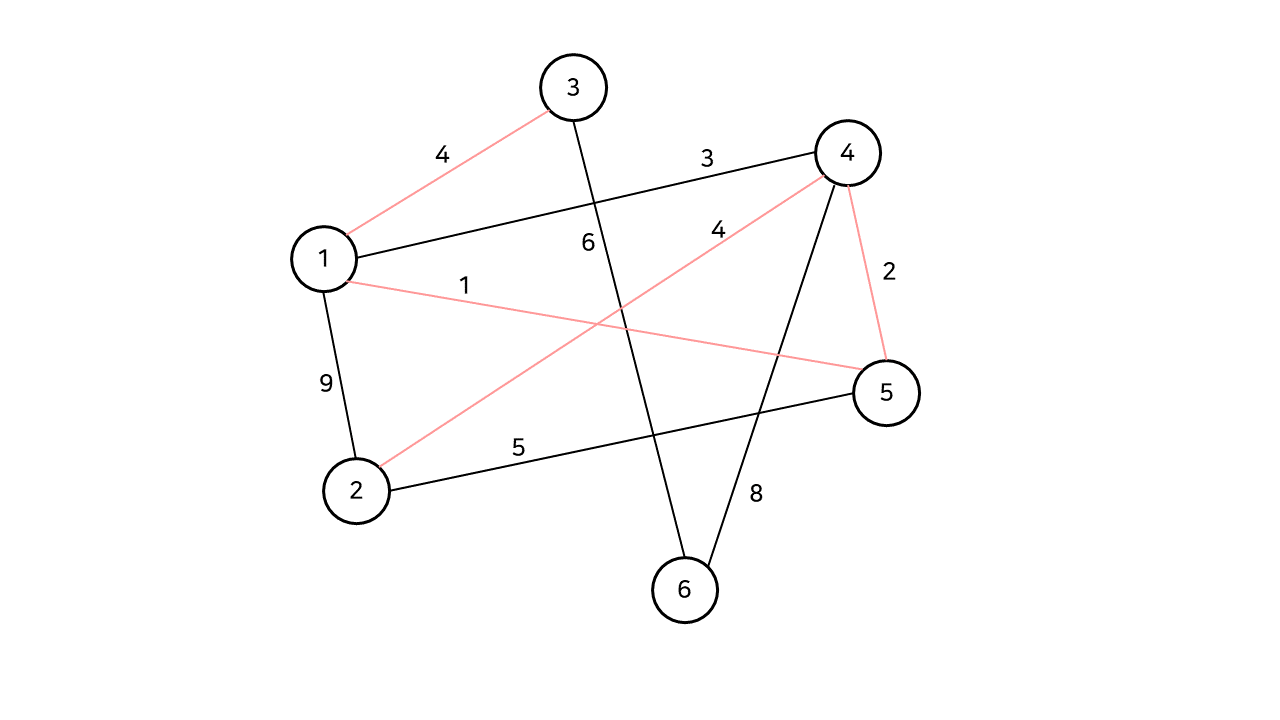
아직 선택되지 않은 간선들 중 최소 가중치를 갖는 간선을 하나 선택한다. 이번에는 4, 5번 정점을 잇는 간선이 선택되고, 마찬가지로 사이클이 발생하지 않으므로 추가한다.
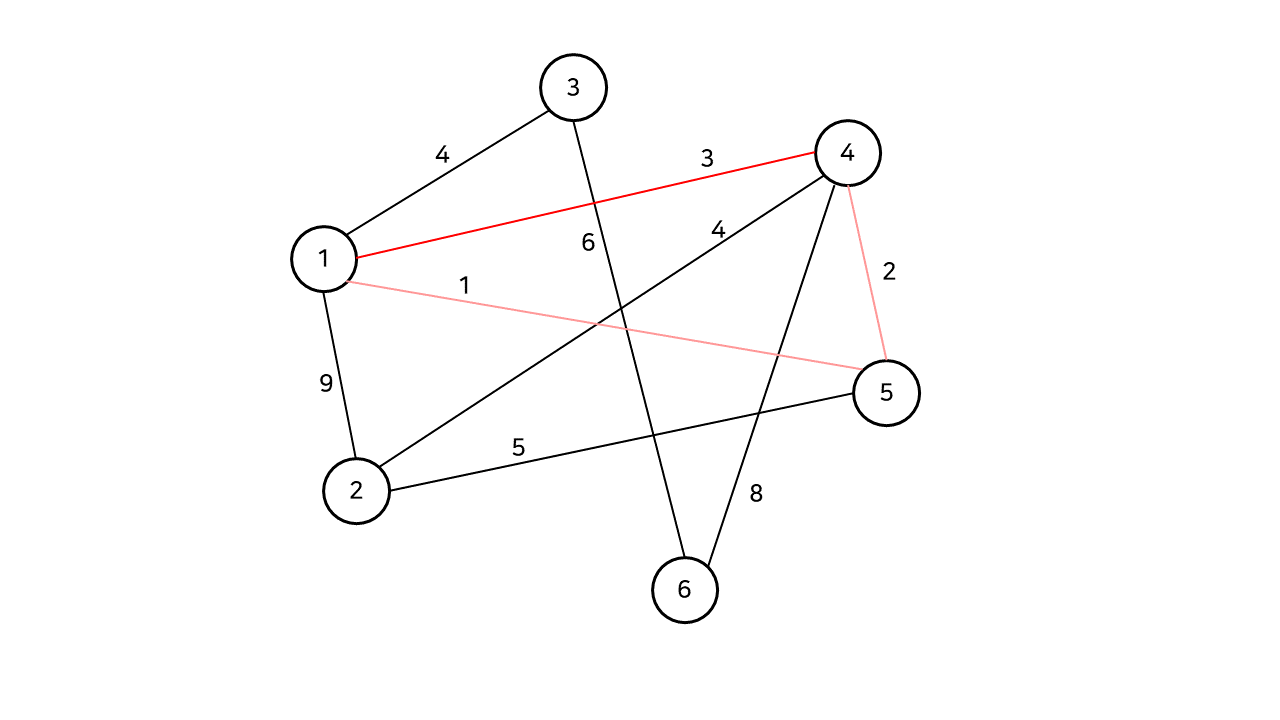
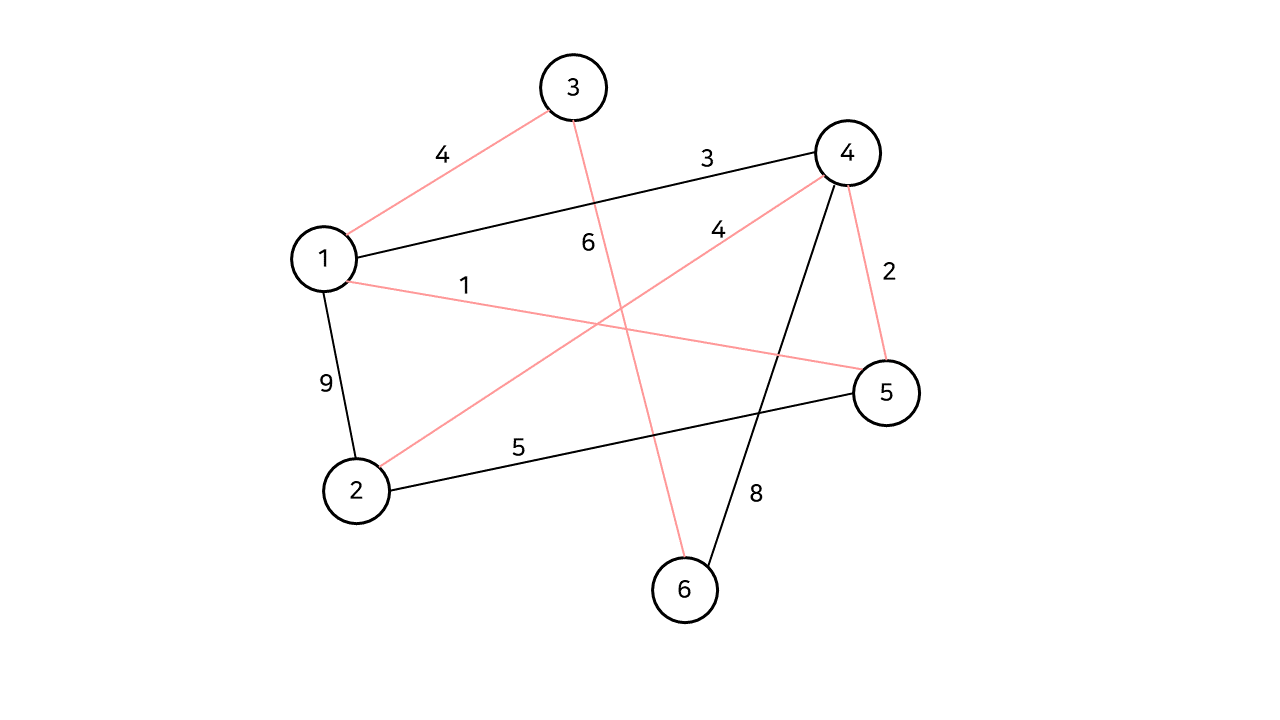
다음으로 1, 4번 정점을 잇는 가중치 3의 간선이 선택되지만, 이 간선을 선택하면 현재까지 구성한 스패닝 트리에 사이클이 발생하게 된다. (1, 4, 5) 따라서 이 간선은 선택하지 않는다. 아래는 완성된 모습.
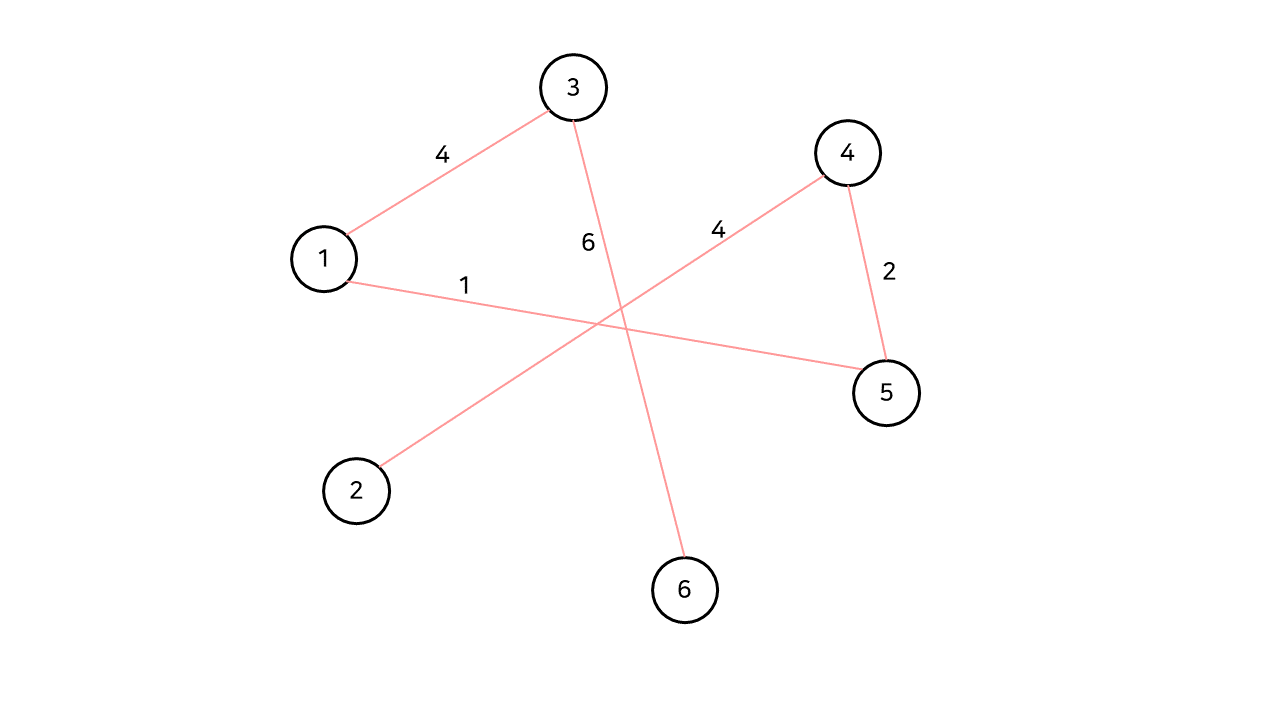
스패닝 트리의 사이클
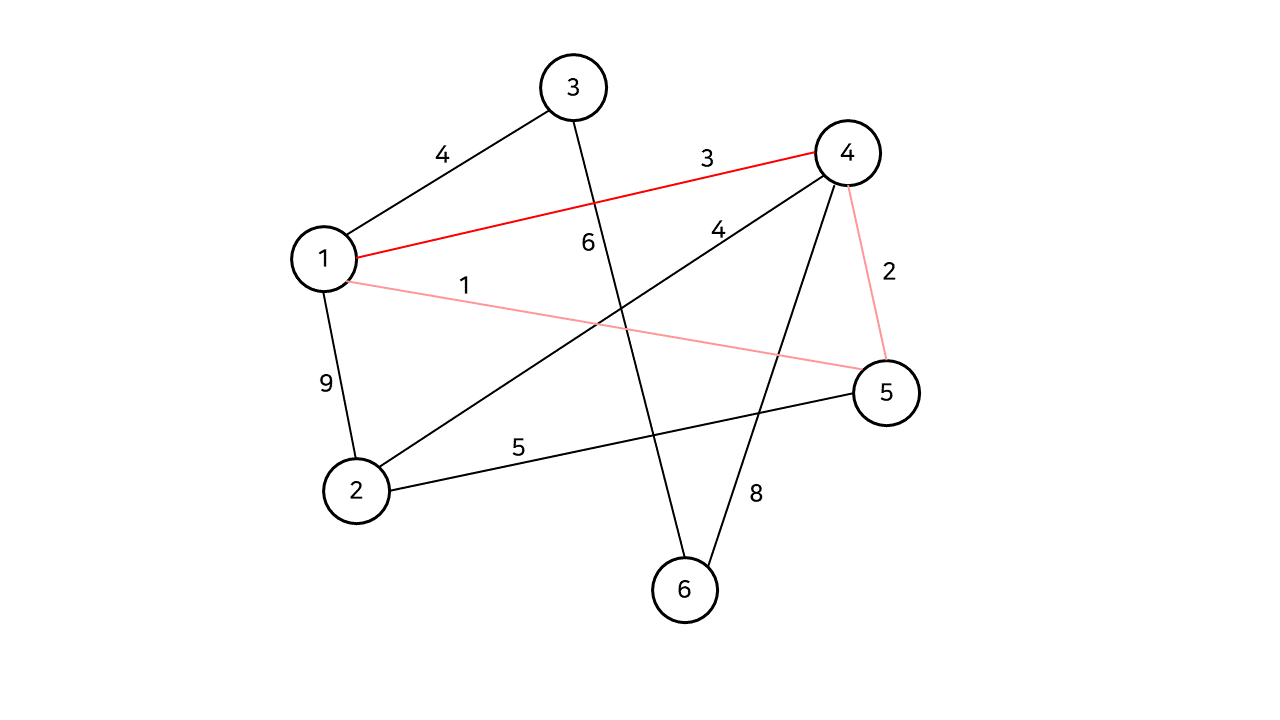
예제 그래프에서 1, 4번 정점을 잇는 간선을 선택했을 때, 우리는 이 간선이 사이클을 발생시키기 때문에 이 간선을 최소 스패닝 트리에 포함시키지 않았다. 구성한 스패닝 트리에 사이클이 발생하는지에 대한 여부를 판단하기 위해, 분리 집합(Disjoint Set)을 사용한다. 이를 실제로 구현하기 위해서 Union-Find 알고리즘을 사용한다.
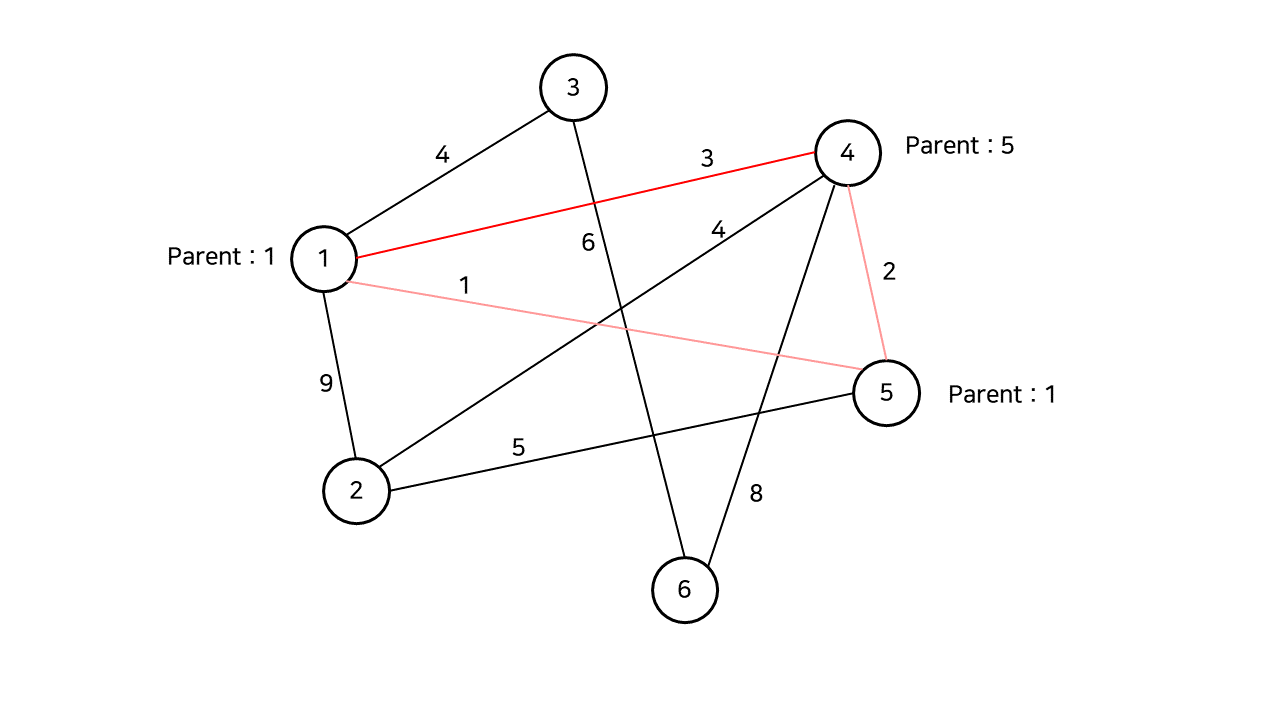
각 간선이 스패닝 트리에 추가될 때마다, Parent 관계를 만들어 놓는다. 만약 어떤 간선을 선택했을 때, 그 간선의 두 정점이 같은 최상위 Parent를 갖는다면 (즉, 같은 그룹에 속했다면) 스패닝 트리에 추가했을 때 사이클이 발생함을 의미한다.
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, pair<int, int>> p;
int v = 6, parent[7];
vector<p> edges;
int find_root(int x) {
if (parent[x] == x) return x;
return parent[x] = find_root(parent[x]); //경로 압축
}
void union_root(int x, int y) {
x = find_root(x);
y = find_root(y);
if (x != y) parent[y] = x;
}
vector<p> kruskal() {
vector<p> mst;
for (int i = 0; i < edges.size(); i++) {
p cur_edge = edges[i];
//현재 간선이 잇는 두 정점
int f = cur_edge.second.first;
int s = cur_edge.second.second;
//Union-Find로 사이클이 발생하는지 확인
if (find_root(f) == find_root(s)) continue; //사이클이 발생한다면 선택하지 않음
//사이클이 발생하지 않는다면 mst에 현재 간선을 추가
mst.push_back(cur_edge);
//Parent 관계 갱신
union_root(f, s);
//만약 정점 개수 v에 대해 v - 1개의 간선을 찾았다면 종료
if (mst.size() == v - 1) return mst;
}
}
void init() {
edges.push_back({ 1, {1, 5} });
edges.push_back({ 4, {1, 3} });
edges.push_back({ 3, {1, 4} });
edges.push_back({ 9, {1, 2} });
edges.push_back({ 4, {2, 4} });
edges.push_back({ 5, {2, 5} });
edges.push_back({ 6, {3, 6} });
edges.push_back({ 2, {4, 5} });
edges.push_back({ 8, {4, 6} });
//간선들을 가중치 기준 오름차순 정렬
sort(edges.begin(), edges.end());
//Union-Find Setting
for (int i = 1; i <= 6; i++) parent[i] = i;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
init();
vector<p> mst = kruskal();
printf("[MST]\n");
for (int i = 0; i < mst.size(); i++) {
printf("%d - %d : 비용 %d\n", mst[i].second.first, mst[i].second.second, mst[i].first);
}
return 0;
}'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| 유향 비순환 그래프 (DAG = Directed acyclic graph) 와 Khan 알고리즘을 이용한 위상 정렬 (Topological Sort) (0) | 2022.08.19 |
|---|---|
| 분리 집합 (Disjoint Set) / Union-Find (0) | 2022.08.14 |
| 가중치 그래프와 임계 경로(Critical Path) (0) | 2022.08.14 |
| C++ vector empty()와 size()간 차이 (0) | 2022.08.04 |
| C++ vector사용법 및 설명 (장&단점) (0) | 2022.08.03 |
