무리수의 곱셈
무리수의 특징은 곱셈이나 나눗셈은 둘 다 루트 안에서 계산이 가능하다는거다. a와 b의 값 둘 다 양수일때 루트a와 루트b를 곱하면 루트ab가 된다, 즉 루트2 * 루트3 = 루트6

a와 b가 모두 양수일 때 루트a 제곱b는 a루트b로 표현이 가능하다
예) 루트12 = 2루트3, 루트18 = 3루트2, 루트24 = 2루트6

제곱근식의 나눗셈

곱셈과 나눗셈이 섞여 있어도 나눗셈은 곱하기를 역수를 취해 계산하면 된다, 단 마지막에는 항상 루트안의 값을 소인수 분해 했을 때 제곱수가 나온다면 제곱하기 전의 값을 항상 밖으로 빼내어 간단하게 정리해야 한다.
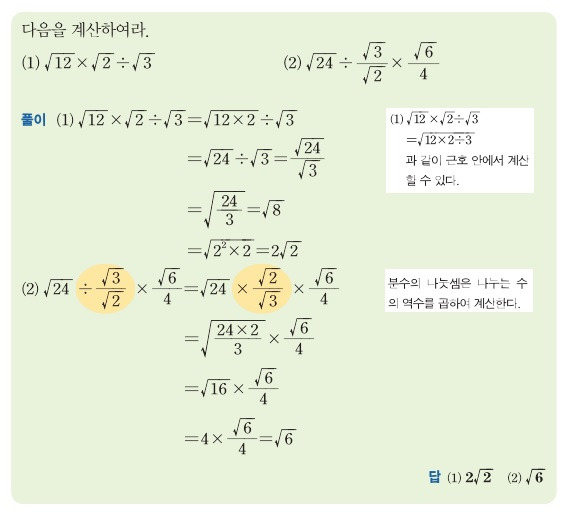
분모의 유리화
분모가 무리수로 되어 있을때, 유리수로 고쳐주는 것이다, 간단하게 설명하면 분모의 값이 근호가 포함된 수가 있을 때, 분모에 있는 같은 무리수의 값을 분모 분자 동시에 곱해주면 된다. 항상 근호가 포함된 식은 간단하게 고쳐줘야 한다.

무리수의 덧셈과 뺄셈
근호 안의 수를 서로 곱하거나 나눠서 근호 안에 나타낼 수 있지만, 덧셈과 뺄셈은 같은 무리수가 있을 때만 가능하다.
예) 루트2 = 1.414, 루트3 = 1.732, 루트5 = 2.236
하지만 루트2와 루트3의 값을 더해서 루트5의 값이 안나오는거와 같이 덧셈은 성립되지 않는다.

괄호가 포함된것도 똑같이 계산해주면 된다

합차 공식을 이용한 분모의 유리화
분모에 무리수만 있다면 같은 무리수를 곱하면 되지만 무리수와 유리수가 더한값이 나온다면, 아무리 무리수의 값을 곱해도 계속 무리수가 나오게 된다, 그럴때는 곱셈 공식의 합차공식을 이용하면 분모에 유리수의 값만 나오게 된다.

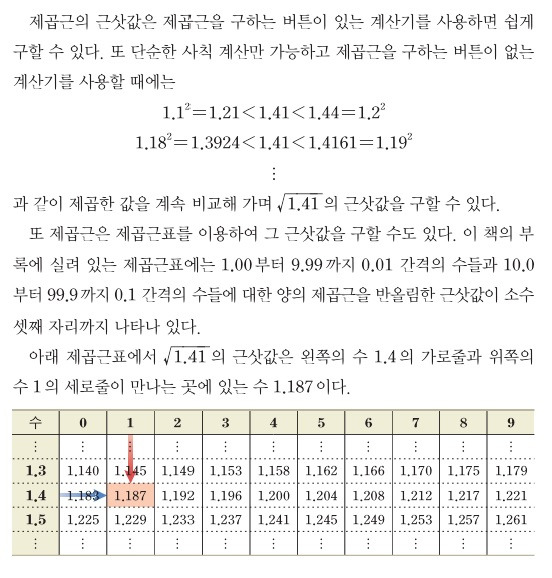
제곱근 표를 보고 찾는 방법
1.00부터 9.99까지 0.01 간격의 수
10.0부터 99.9까지 0.1 간격의 수
에 대한 제곱근의 값을 반올림하여 소수 셋째 자리까지 나타낸 표다.
세로줄에 맨 왼쪽에 있는 숫자가 처음의 2개 숫자를 나타내고 가로의 숫자가 2개 다음의 3번째 숫자를 나타낸다.
아래 예시에서 루트 1.41의 근사값은 1.4의 가로줄과 1의 세로줄을 찾으면 1.187이 루트 1.41의 값이 된다
100이 넘는 수나 소수점의 수도 쉽게 구할 수 있다
루트 100 = 10, 루트 10000 = 100

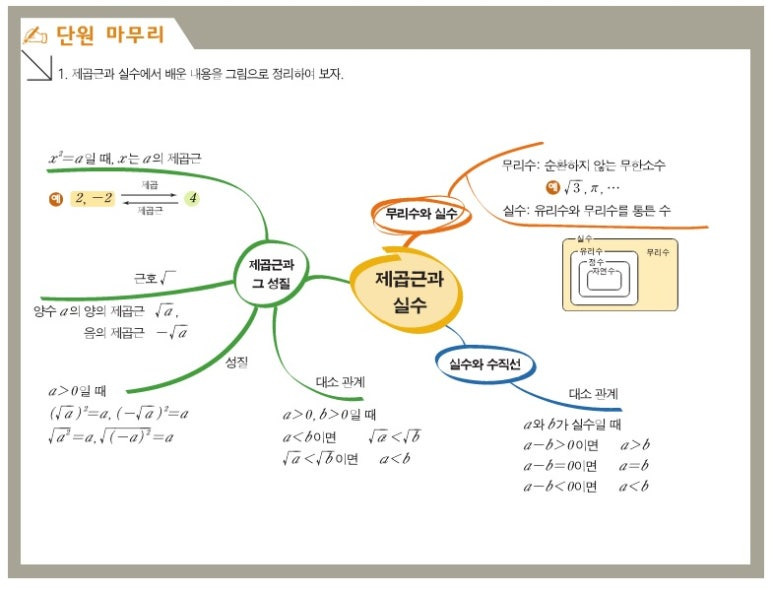
제곱근과 실수
'그래픽스 > 수학 물리' 카테고리의 다른 글
| 최대공약수와 최소공배수의 관계 (0) | 2024.08.28 |
|---|---|
| 최대공약수와 최소공배수란 (0) | 2024.08.28 |
| 소인수분해로 약수 구하는 문제풀이 (0) | 2024.08.28 |
| 소인수분해로 약수 구하는 법 (0) | 2024.08.28 |
| 소인수분해로 약수의 개수 구하는 문제 풀이 (0) | 2024.08.28 |
