서로 다른 두 자연수라도 약수를 구해보면 똑같이 공통된 약수가 있다. 예를 들어 자연수 12와 18의 약수를 구해보면 아래와 같은데, 이 중에서 1, 2, 3, 6은 똑같이 공통된 약수다, 그리고 이렇게 서로 다른 두 자연수의 공통된 약수를 보통 공약수라고 한다.

또 공약수 중에서 가장 큰 수를 최대공약수라고 하는데, 자연수 12와 18의 최대공약수는 6이다.

최대공약수를 알면 공약수 구하기가 쉬워진다 왜냐면 최대공약수의 약수가 바로 공약수이기 때문이다, 그래서 일일이 약수를 구해서 공약수를 찾지 않아도, 최대공약수만 알면 쉽게 공약수를 구할 수 있다. 물론 12와 18의 경우에는 숫자가 작아서, 공약수를 일일이 구해도 상관없지만, 숫자가 클 경우에는 공약수 구하기가 번거롭다. 예를 들어 자연수 1800과 2700의 공약수는 숫자가 너무 커 구하기가 힘들 것이다, 그래서 최대 공약수를 구한 다음, 해당 최대공약수의 약수를 찾으면 수월하게 구할 수 있다. (1800과 2700의 최대공약수는 900이고, 900의 약수를 구하면 된다.

그런데 숫자 1을 제외하면 서로 공약수가 없는 경우도 있다. 예를 들어 자연수 2와 7은, 1을 제외하면 서로 공통된 약수가 없다. 마찬가지로 자연수 3과 5는, 1을 제외하면 서로 공통된 약수가 없다. 이렇게 숫자 1을 제외하고 서로 공통된 약수가 없는 수를 서로소라고 하는데, 서로 기본 바탕이 다르다는 뜻이다. 어차피 1은 모든 자연수의 약수이므로 약수로 1이 없는 수는 없다, 그래서 1을 제외하면, 애초에 기본 바탕이 다르기에 공통된 약수가 없는 것이다.

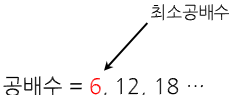
최소공배수는 먼저 공약수와 마찬가지로 서로 다른 두 자연수라도 배수를 구해보면 똑같이 공통된 배수가 있다. 예를 들어 자연수 2와 3의 배수를 구해보면 아래와 같은데, 이 중에서 6, 12, 18 ...은 똑같이 공통된 배수(공배수)다.

또 공배수 중에서 가장 작은 수를 최소공배수라고 부르는데, 자연수 2와 3의 최소공배수는 6이다.
그리고 최대 공약수와 마찬가지로, 최소공배수를 알면 공배수 구하기가 쉬워진다 왜냐면 최소공배수의 배수가 바로 공배수이기 때문이다, 그래서 최소공배수인 6의 배수를 구해보면 자연수 2와 3의 공배수를 쉽게 구할 수 있다.
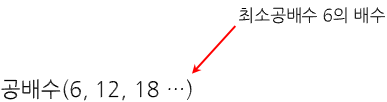
'그래픽스 > 수학 물리' 카테고리의 다른 글
| 근호를 포함한 식의 곱셈과 나눗셈, 덧셈과 뺄셈 개념 정리 (0) | 2024.09.03 |
|---|---|
| 최대공약수와 최소공배수의 관계 (0) | 2024.08.28 |
| 소인수분해로 약수 구하는 문제풀이 (0) | 2024.08.28 |
| 소인수분해로 약수 구하는 법 (0) | 2024.08.28 |
| 소인수분해로 약수의 개수 구하는 문제 풀이 (0) | 2024.08.28 |
