수직선 상의 두 점 사이의 거리
점 A와 점 B사이의 거리는 5 - 2 = 3 B의 좌표에서 A의 좌표를 뺀 값이다.
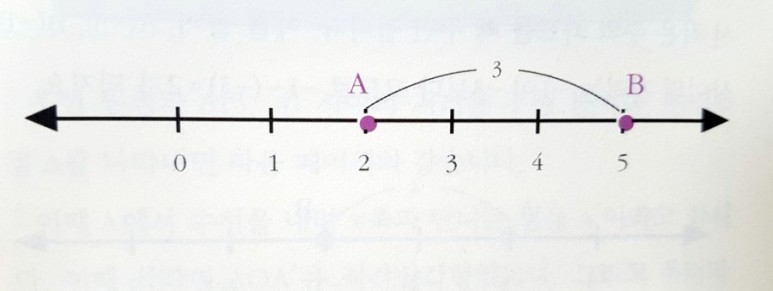
그렇다면 좌표가 음수인 경우는 어떨까?
A와 B 사이의 거리는 1-(-1)=2이지. 그러므로 수직선에서의 두 점 사이의 거리는 큰 수의 좌표에서 작은 수의 좌표를 빼 주면 된다
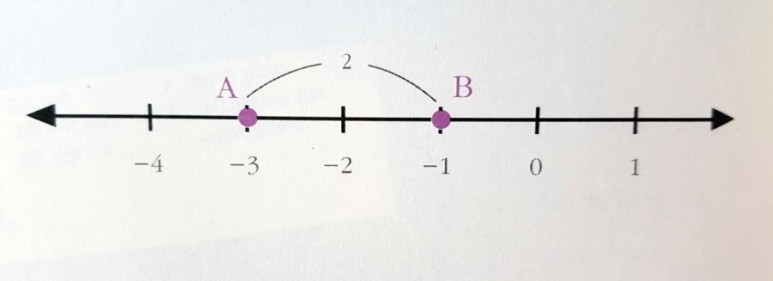
두 점 모두 음수 좌표인 경우도 마찬가지로 구할 수 있다 A(-3)과 B(-1) 사이의 거리는 -1이 -3 보다 크므로 -1-(-3)=2가 된다.
평면상의 두 점 사이의 거리 공식
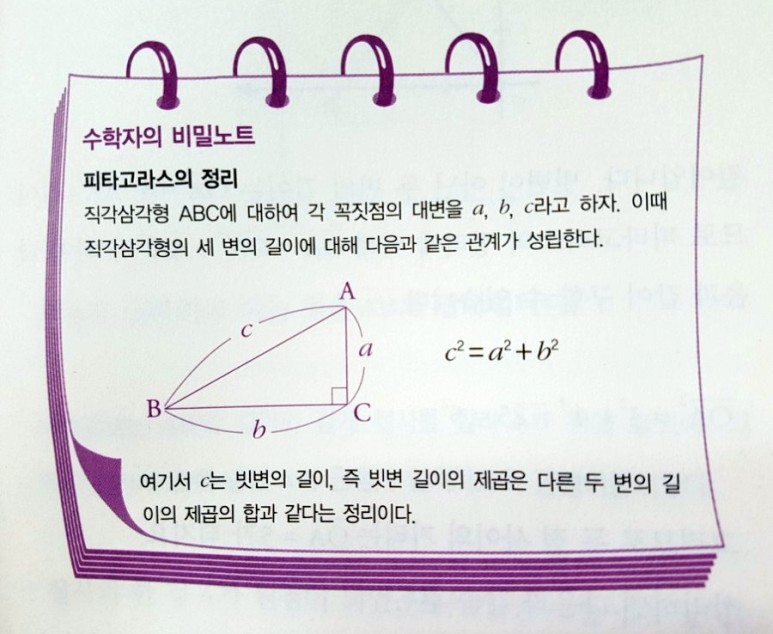
직각삼각형 ABC에 대해 각 꼭짓점의 대변을 a,b,c 라고 할 때 직각삼각형의 세 변의 길이에 대해 다음과 같은 관계가 성립한다. c^2 = a^2 + b^2 여기서 c는 빗변의 길이다, 즉 빗변의 길이의 제곱은 다른 두 변 길이의 제곱의 합과 같다.
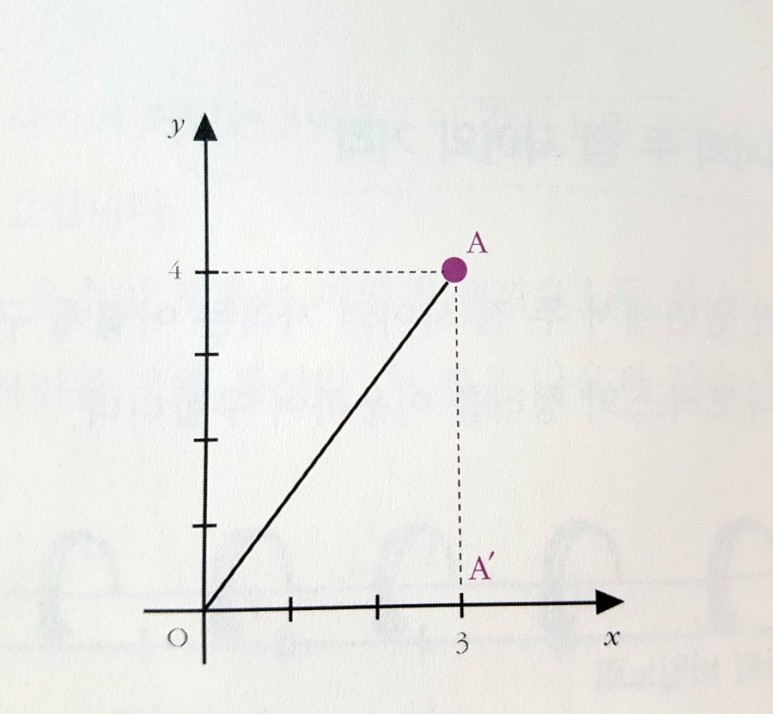
먼저 원점과 점A(3,4) 사이의 거리를 구해보자.
점 A에서 수선을 내려 x축과 만나는 점을 A이라고 한다면, 구하고자 하는 선분OA가 직각삼각형 AOA의 빗변이므로 AO^2+AA^2=OA^2가 성립된다 따라서 3^2+4^2=OA이고, 식을 풀면 두 점 O와 A사이의 거리가 5라는걸 구할 수 있다.
그렇다면 원점이 아닌 두 점 사이의 거리는 어떻게 구할까?
이 경우도 마찬가지다, 예를 들어, 점 A(1,2)와 B(4,6) 사이의 거리를 구해보자, 선분 AB를 점 A가 원점에 가도록 평행 이동시키면
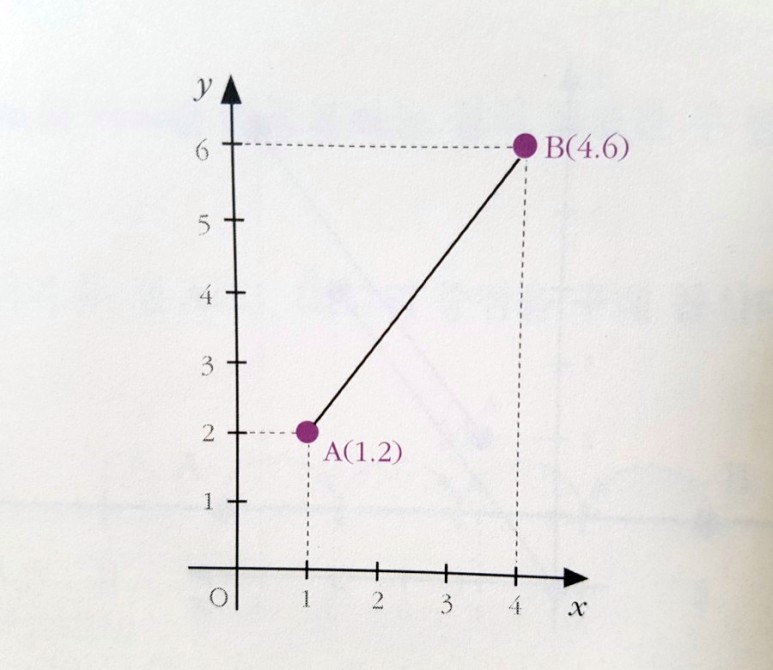
다음과 같이 OB이 된다. 점 A가 원점으로 이동하기 위해서는 x축의 방향으로 -1만큼, y축의 방향으로 -2만큼 평행 이동시키면 되므로 점 B도 똑같이 이동시켜서 (3,4)의 위치로 가게 하면 아까와 똑같은 삼각형이 나오고 선분 AB의 길이는 피타고라스의 정리를 써서 마찬가지로 5임을 구할 수 있다.
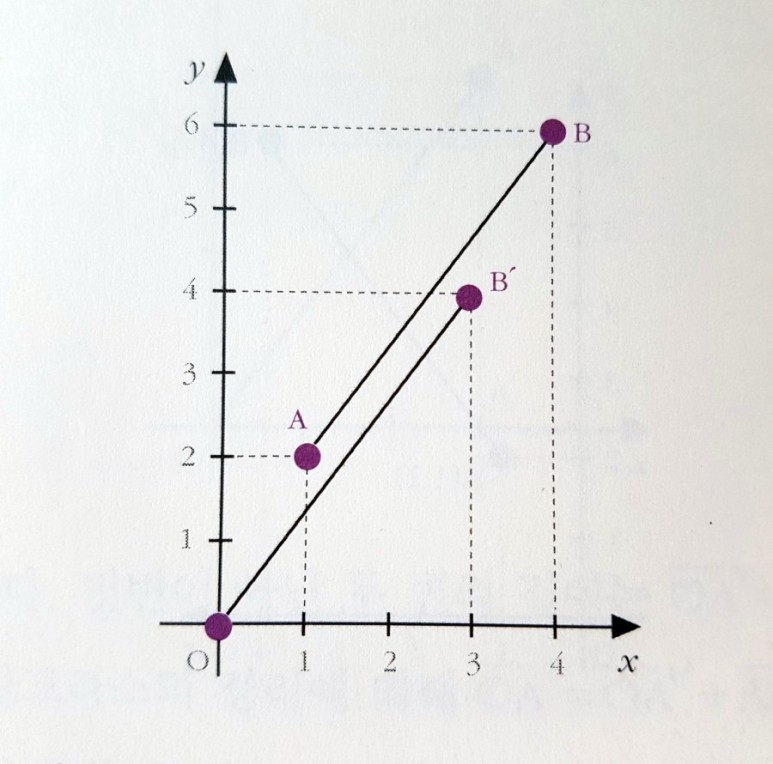
정리하면
(두 점 사이의 거리)^2=(두 점의 x좌표의 차)^2+(y좌표의 차)^2
AB^2=(4-1)^2+(6-2+^2=25=5^2=5
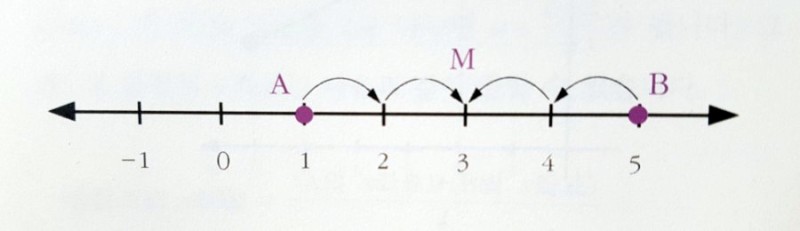
수직선 상의 중점 구하기
두 점 사이의 중점을 M이라고 하면 A에서 M까지의 거리와 M에서 B까지의 거리는 모두 4/2=2가 된다, 따라서 점 A(1)에서 2만큼 간 점이 바로 중점인 M(3)이 되는거다. 여기서 3이란 값은 A의 좌표와 B의 좌표를 더한 6을 2로 나눠서 구한 값이다. 그러므로 중점의 좌표는 두 점의 좌표의 합을 2로 나누어서 구할 수 있다.
M의 좌표=(A의 좌표+B의 좌표)/2
평면 상의 중점 구하기
A(2,4)와 B(6,2)의 중의 좌표를 M(a,b)이라고 하고
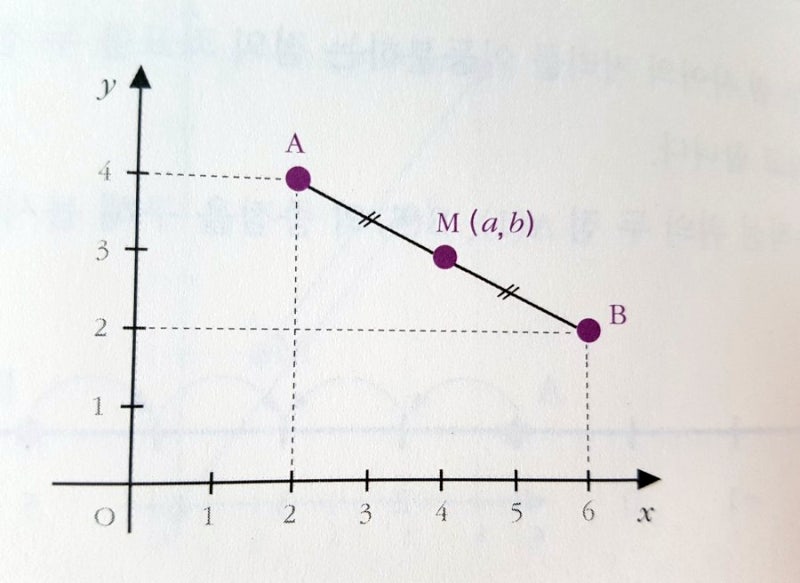
A, M, B에서 각각 x축에 내린 수선과 x축이 만나는 점을 A', M', B'라고 해보자.
수선을 내려도 x좌표는 변하지 않으므로 A'(2,0), M'(a,0), B(6,0)라고 할 수 있고 A'M'의 길이는 a-2, M'B'의 길이는 6-a인데
AM의 길이와 MB의 길이가 같으므로 A'M'의 길이와 M'B'의 길이도 같음을 이용하면 a-2=6-a -> 2a=2+6이고 양변을 2로 나누면 a=(2+6)/2=4 라는 중점의 x좌표를 구할 수 있다. 즉, 중점 M의 x좌표=(점 A의 x좌표+점 B의 x좌표)/2 이다.
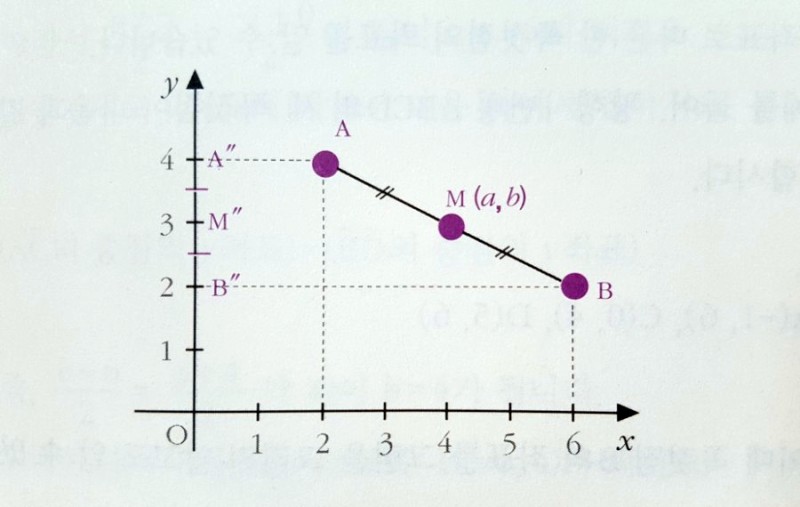
중점의 y 좌표도 구해보자. 이번에는 A, M, B에서 y축으로 수선을 내리는거다.
각각 만나는 점을 A'', M'', B''이라고 하면 A''(0,4), M''(0,b), B''(0,2)가 되고 이 때 AM의 길이와 MB의 길이는 같으므로 A'M''의 길이와 M''B''의 길이도 같다. 즉, A''M''의 길이는 4-b이고 M''B''의 길이는 b-2이므로 4-b=b-2 -> 2b=2+4이고, 양변을 2로나누면 b=(2+4)/2=3 이고 위와 마찬가지로 중점 M의 y좌표= (A의 y좌표+B의 y좌표)/2 라는 걸 알 수 있다
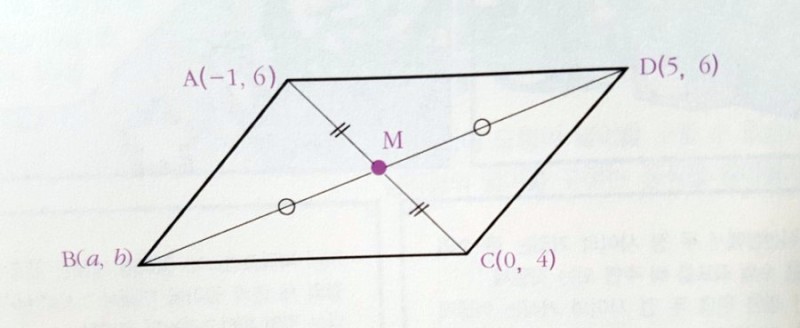
평행사변형에서 주어진 세 꼭짓점의 좌표로 다른 한 꼭짓점의 좌표를 구할 수 있다.
예를 들어, 평행사변형 ABCD의 세 꼭짓점이 다음과 같다고 해보자. A(-1,6), C(0,4), D(5,6) B의좌표를 (a,b)라고 해보자.
평행사변형은 두 대각선이 서로를 이등분한다는 성질이 있다 두 대각선이 만나는 점 M이 선분 AC의 중점이면서 동시에 선분 BD의 중점이라는 거다. 이렇게 두 선분의 중점이 일치하기 때문에 다음 식이 성립한다. 선분AC 중점의 x좌표 = 선분 BD 중점의 x좌표. 따라서 a+5/2=(-1+0)/2 이고, 식을 풀면 a=-6 마찬가지로 y좌표의 식도 성립한다. 즉, b+6/2 =6+4/2가 되어 b=4가 됨으로서 꼭짓점B의 좌표는 (-6,4)가 되는거다.
'그 외 > Math' 카테고리의 다른 글
| 일차방정식 개념정리 (0) | 2024.12.22 |
|---|---|
| 곱셈 공식 & 인수 분해 공식 (0) | 2024.12.22 |
| 단항식 다항식 (1) | 2024.12.22 |
| [수학] 순열, 조합 공식 총 정리 (0) | 2023.10.09 |
