아핀 변환 Affine Transformation

어떤 모델이든 아핀 공간에 있는 모델들은 점들의 집합이라고 했다. 그 점들이 어떤 식으로 있느냐가 모델을 만든다고 했다. Vertex가 모여 모델을 이룬다. 점들의 개수에 따라 모델의 질이 달라진다.

그 점 중에서도 모델을 위치시키기 위해서 다른 점이 하나 더 필요하다. 바로 중심점이라는 것이다. 중심점을 기준으로 나머지 점의 위치를 상대적으로 표현한다.

이 큐브에서는 중심점을 원점에 위치해 놓았다.

 

원점에서 각 점으로 향하는 8개의 벡터가 있다고 하자. 만약 크기를 어떤 축으로 늘리고 싶으면 8개의 벡터에 해당 축에 해당하는 크기 변환 행렬을 적용한다. 그렇게 되면 8개 벡터에 대한 새로운 벡터가 나오고 다시 벡터의 끝 점이 원점의 기준에 의해 바뀔 것이다.

 

벡터를 크기 변환한 것이 점을 크기 변환한 것 같이 된 것이다.

 

모델의 중심점이 원점에 있을 때 모델의 크기 변환은 모델을 이루는 점들을 벡터처럼 생각하고 적용하면 그렇게 된다.

 

회전변환도 동일하게 벡터에다 회전 변환을 적용하면 점이 회전한 것처럼 보이게 된다.

 

중심이 원점이 아닌채로 회전을 할 시

 

아핀 공간에 존재하는 모델의 크기, 방향 변환할 때  중심점의 위치에 따라 달라진 결과를 보였다.

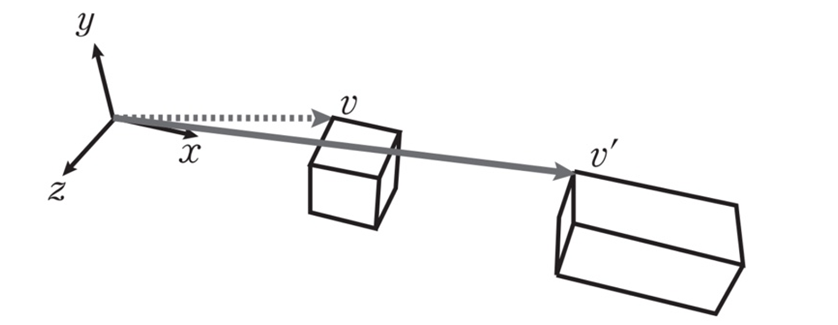
아핀 변환을 사용한 선형 매핑 방법

아핀 변환은 점, 직선, 평면을 보존하는 선형 매핑 방법입니다. 아핀 변환 후에도 평행한 선들은 평행한 상태로 유지됩니다.아핀 변환 기술은 이상적이지 않은 카메라 각도에서 발생하는 기하학적 왜곡이나 형태 변형을 보정하는 데 주로 사용됩니다. 예를 들어, 위성 영상에서는 광각 렌즈 왜곡, 파노라마 스티칭, 영상 정합을 보정하는 용도로 아핀 변환을 사용합니다. 영상을 변환하고 결합하여 크고 평평한 좌표계로 옮겨 놓으면 왜곡을 제거하기에 좋습니다. 이렇게 하면 영상 왜곡을 고려하지 않고 상호 작용 및 계산을 쉽게 수행할 수 있습니다.

 

아핀 변환 표

 

Affine Transfomation(아핀 변환, 어파인 변환) 비례를 유지하는 s-기하학적 함수를 아핀 변환이라고 합니다.

 

 

 

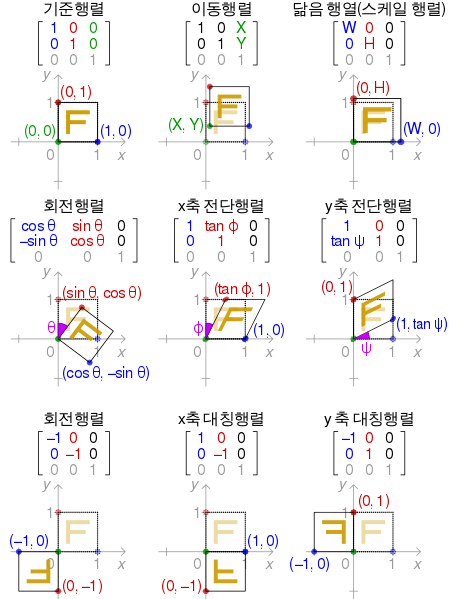
출처 : https://luv-n-interest.tistory.com/810

https://kr.mathworks.com/discovery/affine-transformation.html

https://koreapy.tistory.com/1078