1. 폴리곤 메쉬(Polygon Mesh)란?

그래픽스에서 렌더링(표현)할 물체의 표현을 만드는 작업을 "모델링"이라고 한다. 한 예로 구를 표현하려면 좌측 그림처럼 구의 중점과 반지름을 가지고 우리가 아는 구의 방정식을 세울 수 있다 흔히 이런 형태의 함수는 음함수(Implicit Function)라고 하는데, 음함수는 GPU로 표현하기 어렵다. GPU에서 표현하기 어렵다는 이유 때문에 이런 음함수 표현 대신 부드러운 평면의 개수를 샘플링한다. 그러면 일정한 꼭지점이 샘플링 되는데, 그 꼭지점들을 선으로 이어서 다각형으로 만든 것을 대신 표현한다. 이렇게 도형 그 자체를 표현한 것이 아니라, 꼭지점을 샘플링해 선으로 이은 다각형을 폴리곤 메쉬라고한다. (GPU는 이러한 폴리곤 메쉬를 처리하는데 아주 최적화 되어있다)
+) 음함수란?
일반적으로 f(x)=2x+1f(x)=2x+1과 같이 종속변수와 독립변수가 분리된 함수를 양함수라고 하고, 반대로, f(x,y)=rf(x,y)=r과 같이 종속변수와 독립변수가 분리되지 않은 함수를 음함수라고 부른다.
2. 메쉬의 종류 (삼각 vs 사각)
가장 간단한 다각형은 삼각형이다(변의 수가 가장 적기 때문) 삼각형으로 만든 폴리곤 메쉬를 Triangle Mesh라고 부르며, 실제로 가장 많이 쓰이는 메쉬이다 (OpenGL ES도 이렇게 처리한다) 보통적으로 꼭지점 개수가 n개면 삼각형의 수는 최대 2n개가 생긴다 (오일러 공식에 의하면 그렇다) 그런데 실제로 모델링 단계에서는 삼각형 메쉬보다 사각형 메쉬를 쓰는 것이 훨씬 유리하다.
https://www.youtube.com/watch?v=ac4qV2uIF3Q

삼각형과 사각형 사이의 변환은 매우 쉽다. 삼각형에서 대각선을 전부 제거하면 사각형이고, 사각형에서 한방향으로 대각선을 모두 그려주면 삼각형 폴리곤 메쉬가 된다.
3. 정점의 개수

폴리곤의 정점 개수를 늘리면 오브젝트를 보다 정확하게 표현할 수 있지만, 컴퓨팅이 많아지고 폴리곤의 정점 개수를 줄이면 오브젝트가 부정확하게 표현될 수 있지만, 컴퓨팅이 훨씬 적어진다. 정점의 개수가 곧 Resolution(해상도)가 되는데, 트레이드 오프가 있으니 잘 선택해야한다. 이러한 정점의 수를 그래픽스에서는 LOD (Level of Detail)이라고 한다. 실제로 오브젝트가 화면에 어느정도 크기로 나올지를 생각해서 잘 선택해야한다. 아무리 퍼포먼스가 뛰어난 컴퓨터를 사용한다고 해도 고작 5px정도 하는 구를 표현하기 위해 위 그림에서 가장 오른쪽과 같은 복잡한 메쉬를 선택하는건 효율적이지 못하다. 더 정확하게 정점의 수를 늘리는 것을 Refinement, 줄이는 것을 Silplification이라고 한다.
4. 실제 컴퓨터에선 어떻게 표현될까?
1) Non Indexed Representation
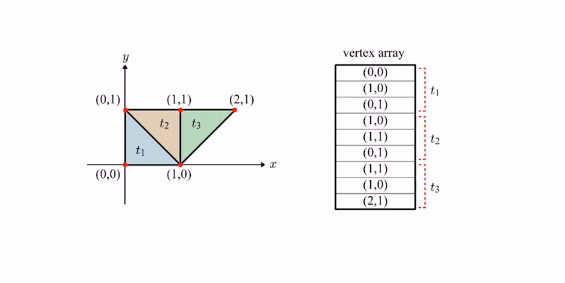
간단하게 보기 위해 2D 메쉬를 예시로 들어서 설명한다. 위처럼 삼각형별로 3칸씩 잡아놓고 좌표를 저장한다 가장 위 3칸은 t1, 그 아래 3칸은 t2, 그 아래 3칸은 t3의 좌표들이 각각 담겨있다. 이렇게 정점의 좌표를 모두 저장하고, 루프를 돌면서 3개씩 끊어서 읽으면 메쉬를 전부 그릴 수 있다. 이러한 배열을 Vertex Array (정점 배열)이라고 한다. 그러나 여기에는 문제가 존재하는데, 중복된 데이터가 굉장히 많다. 예를 들어 (1.0)은 모든 삼각형이 가지고 있는데, 이 (1.0)은 3번이나 중복되어 저장된다.
2) Indexed Representation
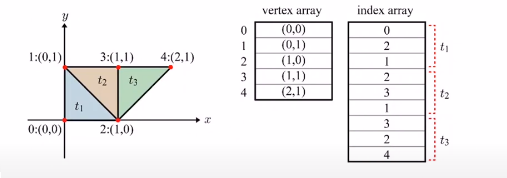
중복을 해결하기 위해 vertex array에는 실제 좌표들을 중복 없이 저장하고, index array를 하나 만들어서, 거기에 vertex array의 인덱스들만 저장하면 훨씬 공간을 절약할 수 있다 vertex array는 integer 2개짜리 struct이고, index는 1개짜리 array이기 때문에 크기가 훨씬 작다 우리가 흔히 사용하는 3차원 폴리곤 메쉬를 사용할 경우, 좌표도 3차원이 되고, 그러면 더 절약할 수 있다. 실제로는 vertex array의 한 셀에는 좌표 이외에도 굉장히 많은 정보들이 있어서 절약률이 상당히 크다.
'그래픽스 > 공통' 카테고리의 다른 글
| 그래픽스 API 정의와 비교 분석 (0) | 2022.09.04 |
|---|---|
| 멀티 스레드 렌더링 (Multi Thread Rendering) (0) | 2022.08.25 |
| 사원수 (Quaternion : 쿼터니언) (0) | 2022.07.25 |
| 짐벌락 & 오일러 각 (Gimbal Lock & Euler Angle) (0) | 2022.07.25 |
| 절두체 컬링 (Frustum Culling)과 클리핑 (Clipping) (0) | 2022.07.03 |
