CS

세그먼트 트리 (Segment Tree)

세그먼트 트리는 "구간을 저장하기 위한 트리" 이다. 예를 들어서 int Array[5] = { 1, 2, 3, 4, 5 } 2번째 값 부터 4번째 값 까지의 합은 2 + 3 + 4로 계산할 것이며 1번째 값 부터 5번째 값 까지의 합은 1 + 2 + 3 + 4 + 5로 계산하게 될 것이다. 특정 구간에 대한 연산이라면, 모든 합을 다 구해놓고 계산하는 방식을 생각할 수 있다. 이걸 1번 연산 이라고 칭하자. 2번 째 값을 7로 바꾸면 { 1, 7, 3, 4, 5 }. 이렇게, 특정 값을 바꾸는 연산 2번 연산 이라고 칭하자. 이 후에 2번째 값부터 4번째 값 까지의 합을 구하고 3번째 값부터 5번째 값 까지의 합을 구하고, 4번째 값을 6으로 바꾸는거와 같은 연산들이 쭉 이어진다고 생각해보자. 별로 문..

이터레이터 Iterator (반복자)

컨테이너에 저장되있는 원소들을 공통적인 방법으로 하나씩 접근할 수 있게 해줌. 모든 컨테이너들이 다 같은 방법으로 반복자 사용 가능. 각 타입에 ::iterator 또는 ::const_iterator 를 뒤에 붙여주면 사용이 가능하다. vector 컨테이너의 반복자 itr vector::iterator itr; vector 컨테이너의 const한 반복자 citr vector::const_iterator citr; 포인터와 비슷하게 사용한다. 간접 참조 가능) itr = v.begin() + 2 에서 *itr 간접 참조를 하면 세번째 원소 값이 리턴된다. iterator 와 const_iterator 의 차이 const_iterator 는 반복자가 가리키는 원소의 값을 변경하지 못한다. 반복자 값이 변경되..

선 중 후 순회 트리

#include using namespace std; #define SAFE_DELETE(x) if(x != nullptr) delete x; // 트리 구조체 typedef struct s_tree_node { char data; s_tree_node* p_left; // 왼쪽 노드에 대한 포인터 s_tree_node* p_right; // 오른쪽 노드에 대한 포인터 public: // 전위 순회 함수 static void Pre_order(s_tree_node* _p_root_node) { if (_p_root_node) { printf("%3c", _p_root_node->data); Pre_order(_p_root_node->p_left); Pre_order(_p_root_node->p_right..

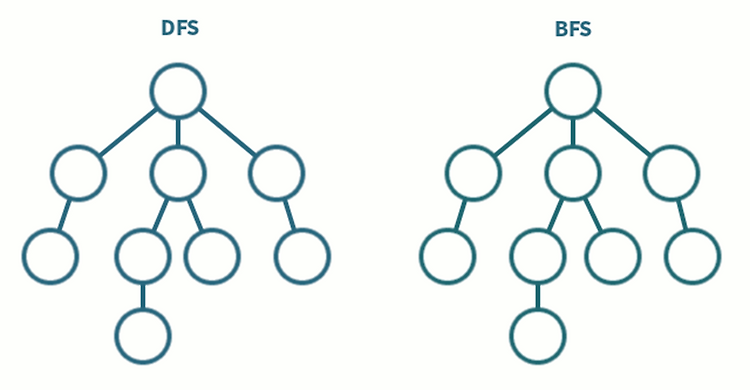
깊이 우선 탐색 BFS / 너비 우선 탐색 BFS 개념

깊이 우선 탐색 (DFS; Depth First Search) 루트 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 알고리즘을 의미한다. 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행한다. 즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색 하는 것이다. 빠르게 모든 경우의 수를 탐색하고자 할 때 사용한다. 스택 이나 재귀함수 로 구현한다. 너비 우선 탐색 (BFS; Breadth First Search) 루트 노드에서 시작해서 인접한 노드를 먼저 탐색 하는 알고리즘이다. 즉, 깊게 (deep) 탐색하기 전에 넓게 (wide) 탐색 하는 것이다. 두 ..

프로세스 메모리 구조와 스택 프레임 구조

프로세스 메모리 구조 프로세스의 메모리 구조는 Text, Data, Heap, Stack 영역으로 구분되어 있다. 프로세스 메모리 구조 Text 영역 : 프로그램 코드와 상수가 정의되어 있고, 읽기만 가능한 메모리 영역이기 때문에 데이터를 저장하려고 하면 분할 충돌을 일으켜 프로세스가 중지된다. Data 영역 : 전역 변수(Global variable)와 정적 변수(Static variable)가 저장되어 있는 영역이다. Heap 영역 : 프로그래머의 필요에 따라 동적 메모리 호출에 의해 할당되는 메모리 영역이다. c언어의 기준으로 malloc() 함수나 calloc() 함수에 의해 생성된 변수들이 이 곳에 할당된다. Stack 영역 : 함수 인자 값, 함수 내의 지역 변수, 함수의 반환 주소 등이 저장..

운영체제 프로세스 스레드 메모리 구조

프로그램(Program) 어떤 작업을 위해 실행할 수 있는 파일로 정의할 수 있다. 프로세스(Process) 컴퓨터에서 연속적으로 실행되고 있는 컴퓨터 프로그램 또는 메모리에 올라와 실행되고 있는 프로그램의 인스턴스(독립적 개체) 즉, 운영체제로 부터 시스템 자원을 할당받는 작업의 단위이며 실행된 프로그램을 의미한다. 할당 시스템 자원 CPU시간, 운영시 필요한 주소공간 Code, Data, Stack, Heap의 구조로 되어있는 독립된 메모리 영역 프로세스 메모리 영역 프로세스는 각각 도립된 메모리 영역(Code, Data, Stack, Heap)구조를 할당받게 되며 프로세스당 최소 1개의 메인스레드를 가지고 있다. 각 프로세스는 별도의 주소 공간에서 실행되며, 한 프로세스는 다른 프로세스의 변수나 자..

해시 테이블

해시 테이블은 (Key, Value)식으로 데이터를 저장하는 자료구조 중 하나로 key를 통해 평균 O(1)에 value를 검색할 수 있는 자료구조이다. 해시 테이블은 Key 값을 해시함수(Hash Function)를 사용하여 변환한 값을 색인(index)으로 삼는다. 해시 함수(Hash Function)을 사용해 Key 값을 색인(index)으로 변환하는 과정을 해싱(Hashing)이라고 한다. 해시 함수(Hash Function) 해시 함수의 가장 중요한 점은 고유한 인덱스를 만드는 것이다. 만약 중복되는 인덱스가 발생한다면 이는 충돌(Collision)으로 이어지게 된다. 따라서 해시 함수를 구현하는 해시 알고리즘을 적절히 구현하는 것이 중요하다. 해시 테이블에 사용되는 대표적인 해시 알고리즘에는 ..

레드-블랙 트리(Red-Black Tree)

레드-블랙 트리(Red-Black Tree) 레드-블랙 트리는 자가 균형 이진 탐색 트리이다. 레드-블랙 트리는 다음과 같은 조건들을 만족한다. 1. 모든 노드는 빨간색 혹은 검은색이다. 2. 루트 노드는 검은색이다. 3. 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드) 4. 빨간색 노드의 자식은 검은색이다. == No Double Red(빨간색 노드가 연속으로 나올 수 없다) 5. 모든 리프 노드에서 Black Depth는 같다. == 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다. 레드-블랙 트리 삽입 과정 위 설명만 보고는 레드-블랙 트리가 무엇인지 감이 쉽게 오지 않을 것이다. 레드-블랙 트리를 쉽..

[C] 이진 탐색 트리

이진탐색트리(Binary Search Tree)이란? 이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다. ( #이진트리 - 각 노드의 자식 노드가 최대 2개인 트리) 1. 각 노드에 중복되지 않는 키(key)가 있다. 2. 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다. 3. 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다. 4. 좌우 서브 트리도 모두 이진 탐색 트리여야 한다. 이진 탐색 트리의 특징 이진 탐색 트리는 기존 이진트리보다 탐색이 빠르다. 이진 탐색 트리의 탐색 연산은 트리의 높이(height)가 h라면 O(h)의 시간 복잡도를 갖는다. 이진 탐색 트리 탐색(Search) 이진 탐색 트리의 탐색은 다음과..

트리

트리(Tree)의 개념 트리는 노드로 이루어진 자료구조로 스택이나 큐와 같은 선형 구조가 아닌 비선형 자료구조이다. 트리는 계층적 관계를 표현하는 자료구조이다. 트리는 다음과 같은 특징들을 갖는다. 1. 트리는 하나의 루트 노드를 갖는다. 2. 루트 노드는 0개 이상의 자식 노드를 갖는다. 3. 자식 노드 또한 0개 이상의 자식 노드를 갖는다. 4. 노드(Node)들과 노드들을 연결하는 간선(Edge)들로 구성되어 있다. 트리에는 사이클(cycle)이 존재할 수 없다. 여기서 사이클이란 시작 노드에서 출발해 다른 노드를 거쳐 다시 시작 노드로 돌아올 수 있다면 사이클이 존재한다고 한다. 트리는 사이클(cycle)이 없는 하나의 연결 그래프(Connected Graph)라고 할 수 있다. 트리의 노드는 s..