1. 크기값 (Scale)
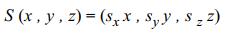
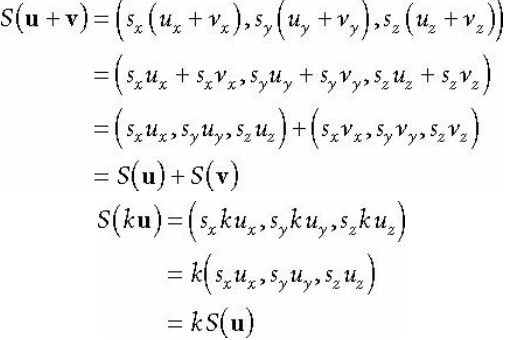
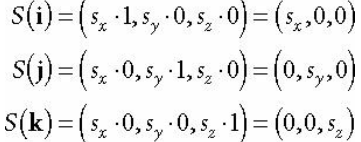
행렬 표현식은 아래와 같다.
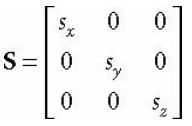
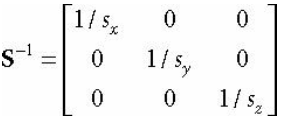

예시2
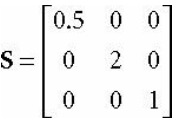
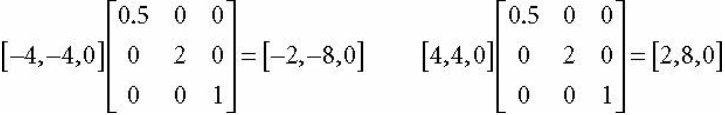
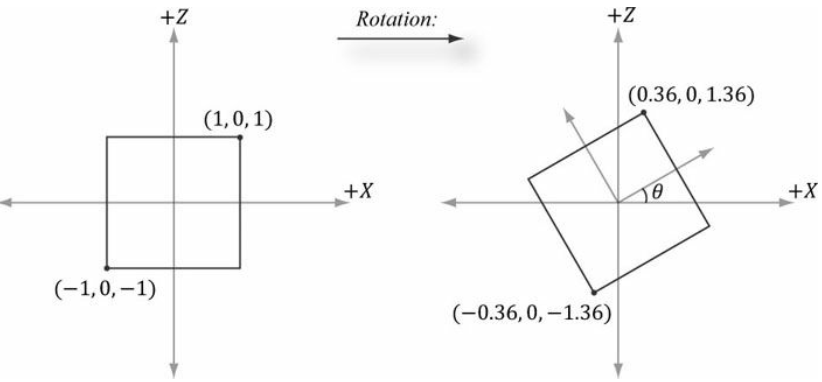
2. 회전값 (Rotation)
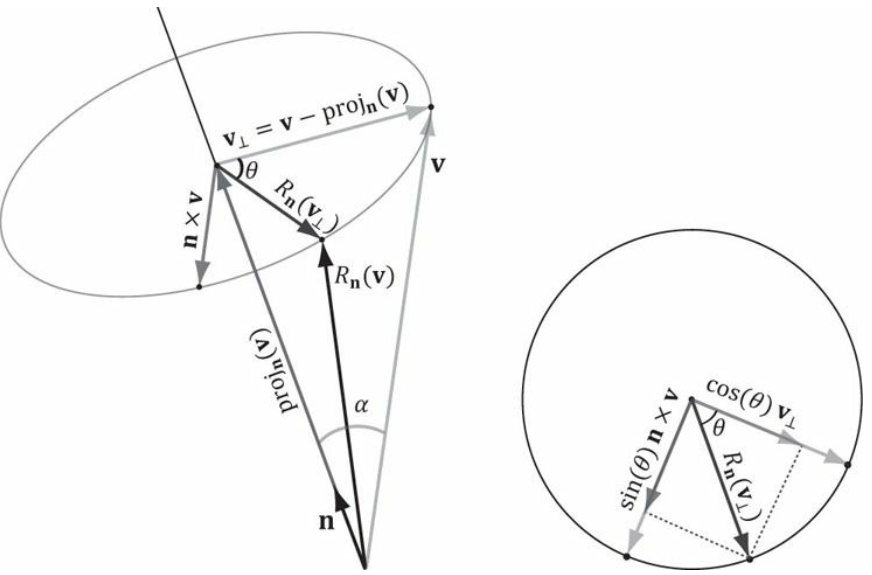
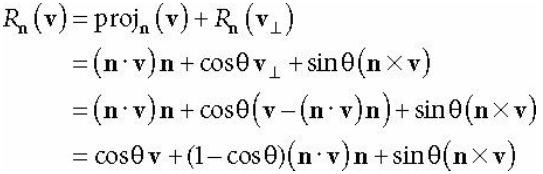
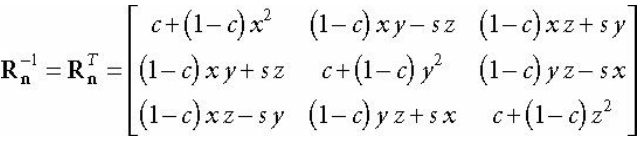

예시 -30도만큼 회전
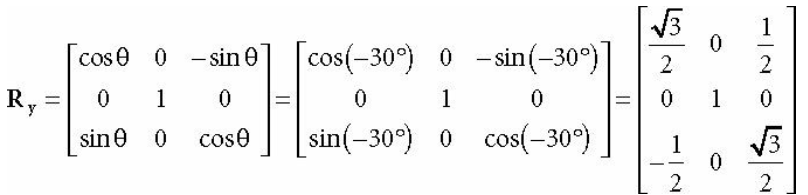
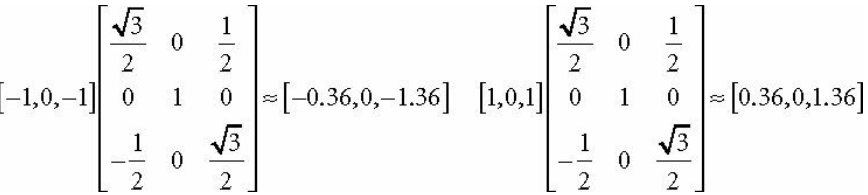
3. 동차 좌표 (homogeneous coordinate)
Homogeneous 좌표는 쉽게 말하면 (x, y)를 (x, y, 1)로 표현하는 것. 임의의 0이 아닌 상수 w에 대해 (x, y)를 (wx, wy, w) 즉, homogeneous 좌표계에서 스케일(scale)은 무시되며 (x, y)에 대한 homogeneous 좌표 표현은 무한히 많이 존재하게 된다. 마찬가지로, 3차원의 경우에는 (X, Y, Z)를 (X, Y, Z, 1) 나 (wX, wY, wZ, w)로 표현.
Homogeneous 좌표가 활용되는 곳은 주로 컴퓨터 그래픽스(graphics) 쪽이나 3D 비전 쪽이다. 그 이유는 homogeneous 좌표계를 사용하면 affine 변환이나 perspective(projective) 변환을 하나의 단일(single) 행렬로 표현할 수 있기 때문.
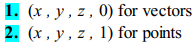
아래는 공식


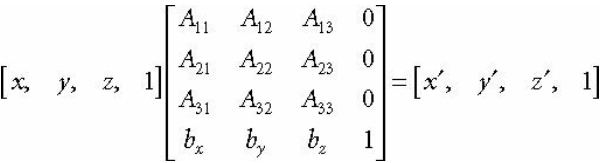
4. 위치값 (Position / Location)
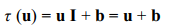
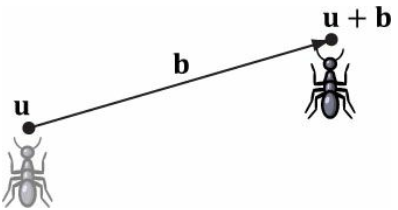
아래는 행렬 기반 예시
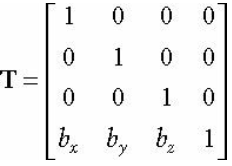

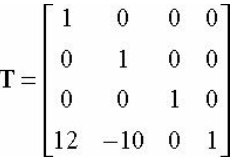
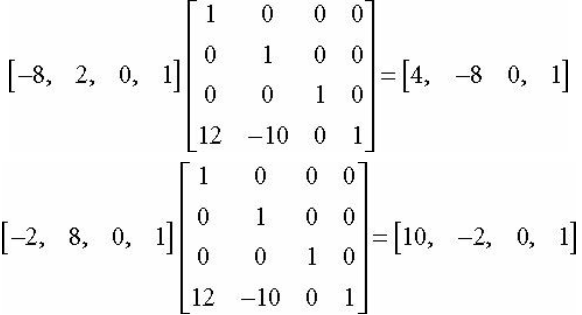
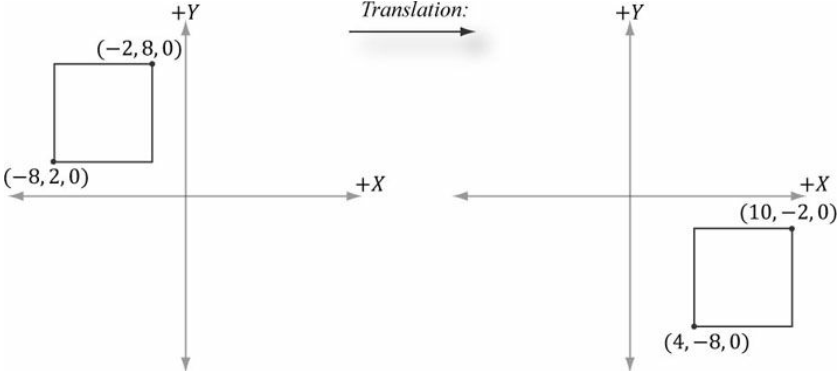
5. 변환행렬 (Affine Matrix)
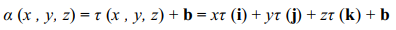
아래는 행렬 예시이다
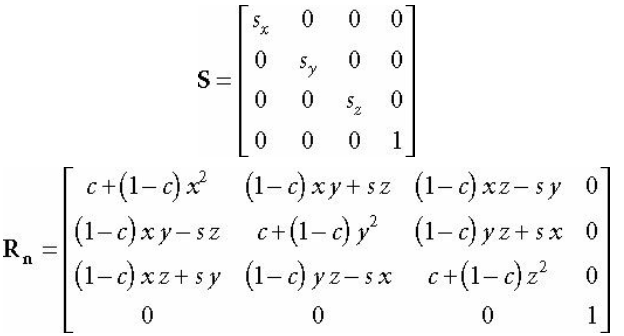
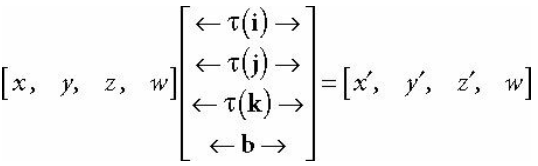


6. 좌표계 변환 (Coordinate Transform)
월드 좌표계(world coordinate system)에서의 점 (X, Y, Z)로부터 카메라 좌표계에서 봤을 때의 좌표 (Xc, Yc, Zc)를 구하는게 목적.
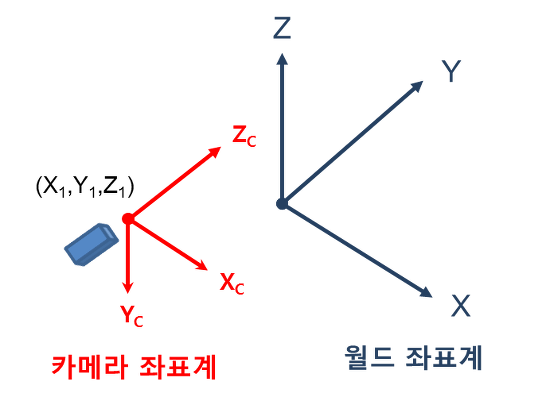
월드좌표계 : 지면이 XY 평면, 위쪽이 Z쪽
카메라 좌표계 : 카메라 광학축 방향이 Zc, 오른쪽이 Xc, 아래쪽이 Yc
또한 월드 좌표계 내에서 카메라의 위치 및 방향을 다음과 같이 정의한다
- 카메라의 위치: 월드 좌표계 내에서 카메라 좌표축 원점의 위치, (X1, Y1, Z1)
- pan(팬): 카메라의 좌우 회전각. 광학축이 월드좌표계 Y축과 평행할때 0도, 왼쪽이 +, 오른쪽이 -
- tilt(틸트): 카메라의 상하 회전각. 광학축이 월드좌표계 Y축과 평행할때 0도, 위쪽이 +, 아래쪽이 -
- roll(롤): 카메라 광학축을 기준으로 한 회전각으로서, 카메라와 같은 방향을 바라볼 때 반시계 방향이 + 방향
즉, 카메라의 pan, tilt는 카메라 광학축(Zc)이 Y축 방향일 때 0이고 카메라를 위로 들면 tilt가 증가, 왼쪽으로 돌리면 pan이 증가.
이제 풀고자 하는 문제를 정리하면 다음과 같다.
카메라의 위치를 (X1, Y1, Z1), 카메라의 팬(pan) 각을 p 라디안, 틸트(tilt)를 t 라디안이라 할 때, 월드좌표계 상의 임의의 점 (X, Y, Z)를 카메라 좌표계 상의 좌표 (Xc, Yc, Zc)로 변환시키는 관계식을 구하라.
좌표계 변환관계는 2가지 방법으로 구할 수 있다. 하나는 일련의 회전변환 행렬을 조합하는 것이고, 다른 한 방법은 단위벡터를 이용해 직접 변환행렬을 구하는 것이다.
방법 1: 회전변환을 조합하는 방법
월드 좌표축을 카메라 좌표축 방향과 일치되도록 하는 회전변환 행렬을 R이라 하면, R은 아래와 같이 구해진다 (3D 회전변환 행렬에 대해서는 [컴퓨터 비전에서의 Geometry #5] 3D 변환 참조)
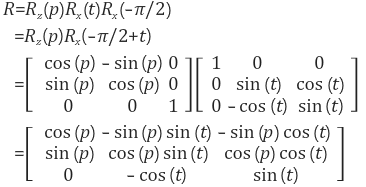
Roll까지 고려한 경우, R = Rz(p)Rx(t)Ry(-roll)Rx(-π/2)로 구해진다. 따라서, 월드좌표를 카메라 좌표로 변환시키는 변환식은 다음과 같이 구해진다.
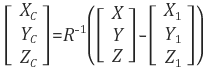
좌표축 변환은 일반적인 변환과정을 역으로 적용함에 주의해야 한다. 회전변환은 RRT = I를 만족하기 때문에 R-1 = RT로 구할 수 있다.
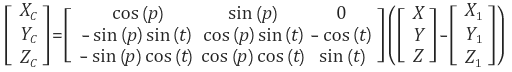
여기서 R은 월드좌표를 카메라좌표로 변환시키는 행렬이 아니라 좌표축을 변환시키는 행렬임에 주의해야 한다. 즉, R은 월드좌표축->카메라좌표축 변환 행렬이다. 좌표로 보면 R은 카메라좌표->월드좌표로 변환시키는 행렬이다 (좌표축 변환과 좌표변환은 서로 역변환 관계). R과 opencv의 solvePnP에서 반환되는 R이 표기가 같아서 서로 혼동스러울 수 있겠지만 solvePnP에서 반환되는 R은 월드좌표->카메라좌표 변환행렬이고, 여기서 정의한 R은 카메라좌표->월드좌표 변환행렬이다. 즉, 서로 반대이다.
방법 2: 변환행렬을 직접 구하는 방법
어떤 선형변환 행렬 T가 있을 때, 각각의 좌표축 단위벡터들이 변환 T에 의해서 어디로 가는지만 알면 T를 손쉽게 구할 수 있다. 만일, T에 의해 X축 단위벡터 (1, 0, 0)이 (a1,a2,a3)로 가고, Y축 단위벡터 (0, 1, 0)이 (b1, b2, b3), Z축 단위벡터 (0, 0, 1)이 (c1, c2, c3)가 된다면, 변환행렬 T는 다음과 같다.
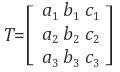
이제, 이 방법를 이용하여 X축을 Xc, Y축을 Yc, Z축을 Zc로 보내는 변환행렬 R을 구하자.
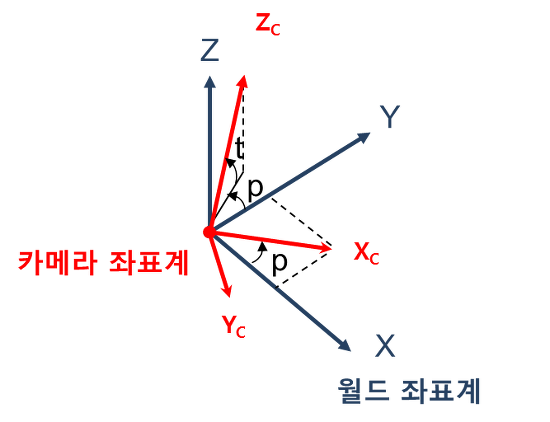
각각의 단위벡터가 어디로 이동해야 하는지를 구해보면 다음과 같다.
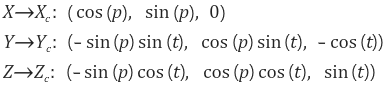
따라서, 변환행렬 R은 다음과 같이 구해진다.
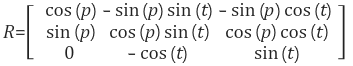
'그래픽스 > DirectX' 카테고리의 다른 글
| [DX11 물방울책] 챕터 5 - 렌더링 파이프라인 (0) | 2022.07.03 |
|---|---|
| DirectX 11 프레임워크 환경 설정하는 방법 (0) | 2022.06.30 |
| [DX11 물방울책] 챕터 4 - Direct3D 초기화 (0) | 2022.06.30 |
| [DX11 물방울책] 챕터 2 - 행렬 (0) | 2022.06.23 |
| [DX11 물방울책] 챕터 1 - 벡터 (0) | 2022.06.22 |
![[DX11 물방울책] 챕터3 - 트랜스폼 (위치값,회전값,크기값)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FAb4gg%2FbtrFzOMrfDq%2FIBNFgD1ZVjKWvuQojcurEK%2Fimg.png)