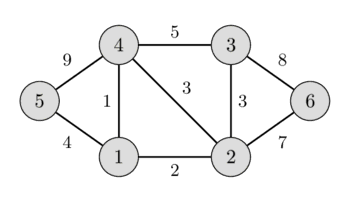
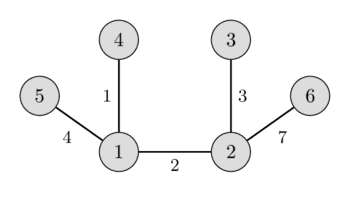
사용할 데이터는 다음과 같다. 결과) 17
1 2 2
2 6 7
3 2 3
3 6 8
4 3 5
4 2 3
4 1 1
5 1 4
5 4 9
공통으로 쓰여짐
// 간선 개수
const int edge = 9;
struct sNode
{
public:
int from = 0, to = 0, weight = 0;
/*sNode() = default;
sNode(int from, int to, int weight) : from(from), to(to), weight(weight)
{
}*/
bool operator<(const sNode& ref) const
{
return weight < ref.weight;
}
bool operator>(const sNode& ref) const
{
return weight > ref.weight;
}
bool operator==(const sNode& ref) const
{
return from == ref.from &&
to == ref.to &&
weight == ref.weight;
}
bool operator!=(const sNode& ref) const
{
return !(*this == ref);
}
};
테스트 하고자하는 알고리즘을 호출하면 된다.
int main()
{
Kruskal kruskal;
Prim prim;
}크루스칼 알고리즘
class Kruskal
{
vector<sNode> graph;
vector<int> parent;
public:
// 초기화
Kruskal()
{
parent.resize(edge + 1);
for (int i = 1; i <= edge; i++)
parent[i] = i;
for (int i = 0; i < edge; i++)
{
int from, to, weight;
cin >> from >> to >> weight;
graph.push_back({ from, to, weight });
}
// 가중치 기준 정렬
std::sort(graph.begin(), graph.end(), [&](sNode from, sNode to)
{
return from < to;
});
int res = 0;
for (int i = 0; i < edge; i++)
{
sNode cur = graph[i];
if (!IsCycle(cur.from, cur.to))
{
res += cur.weight;
Union(cur.from, cur.to);
}
}
cout << res << endl;
}
// 부모끼리 연결
void Union(int from, int to)
{
// parent[Find(to)] = Find(from)과 같음
parent[Find(from)] = Find(to);
}
// 부모를 찾음
int Find(int x)
{
// 같은 부모인지로 걸러내기 때문에 방문여부 배열 불필요
return (parent[x] == x ? x : parent[x] = Find(parent[x]));
}
// 사이클이 존재하는지 확인
bool IsCycle(int from, int to)
{
return Find(from) == Find(to);
}
};프림 알고리즘 (노드 삽입 순서 유의)
우선순위 큐에서 마지막 템플릿 매개변수 predicate는 less<sNode> 사용시 < 연산자 오버로딩이 되어있어야함, 반대로 greater<sNode>는 > 연산자.
class Prim
{
//const int INF = 987654321;
bool Cmp(sNode& lRef, sNode& rRef)
{
return lRef < rRef;
}
// 가중치를 오름차순으로
priority_queue<sNode, vector<sNode>, greater<sNode>> pq;
vector<sNode> graph;
vector<bool> vis;
public:
// 초기화
Prim()
{
vis.resize(edge + 1);
for (int i = 0; i < edge; i++)
{
int from, to, weight;
cin >> from >> to >> weight;
graph.push_back({ from, to, weight });
}
int res = 0;
pq.push(sNode());
// 노드들을 자동으로 정렬해주기 때문에 sort 필요x
while (!pq.empty())
{
auto cur = pq.top();
pq.pop();
// 방문 안한 노드들만
if (vis[cur.from])
continue;
vis[cur.from] = true;
res += cur.weight;
// 현재 노드 기준 방문 안한 노드들이 존재할 수 있기 때문에
for (const auto& node : graph)
{
if (!vis[node.from])
pq.push(node);
}
}
cout << res << endl;
}
};'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [C++] vector resize 시 주의할 점 (0) | 2023.11.22 |
|---|---|
| Brute Force (브루트 포스) 알고리즘 (0) | 2023.11.22 |
| [C++] 삼항 트리를 이중 연결된 목록으로 변환 (0) | 2023.11.06 |
| [C++] Palindrome (팰린드롬 회문)에 대한 모든것 (0) | 2023.11.06 |
| [C++] valarray - 오직 수치값만 저장하는 컨테이너 (0) | 2023.11.05 |
![[C++] 개인적인 (MST 알고리즘) 크루스칼 & 프림 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FxBG4r%2FbtsAmZfycmt%2FgTyK7oWp5t8hyO5XLR3XyK%2Fimg.png)