개념
기존 고지식한 알고리즘과, KMP 알고리즘 혹은 지금까지 봐왔던 알고리즘들은 대부분 처음부터 비교해 나갈 것이지만 보이어-무어 알고리즘은 뒤에서부터 비교해나간다.
뒤에서부터 비교를 진행해 나가다 비교 값이 서로 다를 시 테이블을 참조해 나아간다.
아래는 보이어-무어 알고리즘으로 비교해 나아가는 이미지다.

뒤에서 비교하다 index 3번이 다르다는 것을 확인 후 테이블을 참조한다. 테이블을 참조 후 다음 비교할 위치로 건너뛴다.

그 다음 값을 보면 index 5, 6번이 다르지만 보이어-무어 알고리즘은 뒤에서부터 비교하므로 테이블 참조 시 index 6번에 대한 값을 참조하여 다음 비교 위치로 넘어긴다.

총 2번의 이동만으로 원하는 값을 찾아냈다. 만약 고지식한 알고리즘이었다면 2번 이동했을 때쯤 index 2번에 n의 문자열이 위치했다.
생략 테이블
패턴 문자열을 찾기 위해 패턴 문자열에 대해 생략 테이블이 2개가 필요하다.
첫 번째로는 Bad Character Heuristica 방식으로 (본문 문자에 대해 참조하는)테이블을 생성한다.
하지만 이러한 테이블 만으로는 정상적으로 동작하는 것을 기대하기 어렵기 때문에 두 번째 방식 Good Suffix Heuristica 방식으로 테이블을 생성한다. 이 방식은 KMP 알고리즘과 약간의 유사성이 있다. Suffix, 접미사와 대칭이 되는 것 을 찾아 테이블을 생성하는 방식이다.
1. Bad Character Heuristica
이 방법은 패턴 문자에 대하여 순서대로 번호를 붙여준다. 즉, 비교가 실패하였을 때 만약 그 틀린 본문 문자가 패턴 문자 내에 어딘가에 존재한다면 그곳으로 위치를 변경하는 것이다.
아래는 패턴 문자열에 각각의 번호를 붙여준 모양이다.
(예시가 순서대로 되있지만 중복된 문자가 나올 경우 후에 나온 번호가 뒤집어쓰기 때문에 값이 달라진다.)

그렇다면 위의 테이블을 참조하여 다음의 비교를 진행해보자.

패턴 문자와 본문 문자가 일치하지 않는 부분이 존재한다. 일치하지 낳는 본문 문자는 a 문자이지만 0번에 이미 존재한다.
그럼 다음과 같은 연산을 진행하여 현재의 다음 비교할 위치를 구한다.
다음 위치 = 본문 문자열 내 현재 INDEX + (패턴 문자열 내의 현재 위치 - 테이블에서 참조한 값)

이와 같은 방식으로만 동작하기에는 정상적으로 동작하지 않는 경우도 발생한다. (그 다음에도 일치하지 않는 내용 존재.)
그리고 한 가지 테이블을 더 사용하여 두 테이블 중 더 큰 값으로 넘어간다면 좀 더 반복 횟수를 줄일 수 있을 것이다.
2. Good Suffix Heuristica
이 방식은 접미사와 같은 문자열이 패턴 문자열 내에 존재하는지 를 검사한다. 접미사란 문자열 내에서 시작이 어디든 항상 끝까지 나타낸 문자열을 뜻한다.
아래는 ababcabc에 대한 접미사를 나열한 모습을 보여준다.
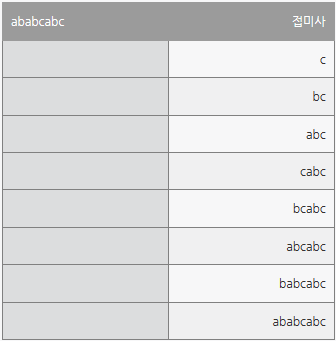
그렇다면 접미사와 일치한다는 문자열이란 아래와 같다.
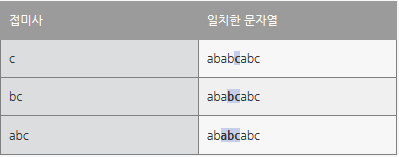
접미사와 같은 문자열이 무엇인지 알았으니 아래 테이블은 위의 내용을 테이블로 만든 내용이다.

접미사와 같았던 문자열이 접미사를 가리키고 있는 것을 확인할 수 있지만 이것만으로 부족하다. 그 이유는 보이어-무어 알고리즘은 뒤에서부터 비교를 해 나아가기 때문에 저 뒤의 접미사 부분이 바뀐다.

나머지 값이 패턴 문자열의 길이인 이유는 보이어-무어는 뒤에서부터 비교하기 때문에 틀리면 패턴의 문자열만큼 과감하게 건너뛸 수 있다. 위의 테이블은 접미사의 인덱스를 나타냈지만 지금 테이블은 다음 인덱스를 얼마큼 더해서 시작할지를 알려준다.
코드
1. Bad Character에 대한 테이블을 정의한다.
Bad Table 은 위에서 설명한 바로 각 문자에 대해 순서대로 번호를 붙여준다고 했다.
const int MAX_SIZE = 256;
vector<int> make_to_bad_character_tb(const string pattern){
const int p_size = pattern.size();
vector<int> bc_tb(MAX_SIZE, p_size);
for(int i = 0; i < p_size; ++i)
bc_tb[(int)pattern[i]] = i;
return bc_tb;
}이 테이블의 문제점은 중복된 문자가 나올 시 기존의 값을 덮어쓴다. 반복문 내용을 보면 받은 문자를 int형으로 바꾼 위치에 값을 저장한다.
2. Good Suffix에 대한 테이블을 만든다.
접미사와 동일해질 때 카운트를 시작하여 그에 맞게 배열에 넣어주는 코드다.
접미사와 동일한 문자들이 접미사의 인덱스를 가르치도록 만드는 작업이 이루어지는 작업과 일치한 접미사를 찾았을 때 그 얼마큼 스킵할지 저장한다.
vector<int> make_to_gs_tb(const string pattern){
const int p_size = pattern.size();
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
suf_tb[pattern_point] = suffix_point;
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
while(pattern_point > 0){
// 접미사가 일치하는 순간 몇개가 일치하는지 카운팅
while(suffix_point <= p_size &&
pattern[pattern_point - 1] != pattern[suffix_point -1]){
if(skip_tb[suffix_point] == 0)
skip_tb[suffix_point] = suffix_point - pattern_point;
suffix_point = suf_tb[suffix_point];
}
// 접미사와 동일한 단어가 접미사인덱스를 가르키도록 설정
suf_tb[--pattern_point] = --suffix_point;
}
...
}
위에서 본 테이블과 많이 비슷해졌지만 아직 생략 테이블은 나머지 문자에 대해서 어떻게 스킵해야 할지 모른다.
suf_tb의 목록을 보시면 일치한 값들이 보인다. 이 값들은 패턴 문자열의 사이즈와 같으면 그 자릿수만큼 생략이 가능하다는 것이다. 그리고 이 값은 앞자리부터 채워준다.

vector<int> make_to_gs_tb(const string pattern){
const int p_size;
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
...
suffix_point = suf_tb[0];
while(pattern_point < p_size){
if(skip_tb[pattern_point] == 0)
skip_tb[pattern_point] = suffix_point;
if(pattern_point++ == suffix_point)
suffix_point = suf_tb[suffix_point];
}
return skip_tb;
}
그리고 이렇게 나온 값으로 원하는 문자열 검색을 한다. 그렇다면 테이블 두 개를 어떠한 방식으로 참조하느냐도 중요하다.테이블을 참조하여 가장 큰 값을 택한다.

#include <iostream>
#include <vector>
using namespace std;
const int MAX_SIZE = 256;
vector<int> make_to_bad_character_tb(const string pattern)
{
const int p_size = pattern.size();
vector<int> bc_tb(MAX_SIZE, p_size);
for (int i = 0; i < p_size; ++i)
bc_tb[(int)pattern[i]] = i;
return bc_tb;
}
vector<int> make_to_gs_tb(const string pattern)
{
const int p_size = pattern.size();
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
suf_tb[pattern_point] = suffix_point;
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
while (pattern_point > 0)
{
cout <<'h'<<endl;
// 접미사가 일치하는 순간 몇개가 일치하는지 카운팅
while (suffix_point <= p_size &&
pattern[pattern_point - 1] != pattern[suffix_point - 1])
{
if (skip_tb[suffix_point] == 0)
skip_tb[suffix_point] = suffix_point - pattern_point;
suffix_point = suf_tb[suffix_point];
}
// 접미사와 동일한 단어가 접미사인덱스를 가르키도록 설정
suf_tb[--pattern_point] = --suffix_point;
}
suffix_point = suf_tb[0];
while (pattern_point < p_size)
{
if (skip_tb[pattern_point] == 0)
skip_tb[pattern_point] = suffix_point;
if (pattern_point++ == suffix_point)
suffix_point = suf_tb[suffix_point];
}
for(auto & suf : suf_tb)
cout << suf << ", ";
cout << endl;
for(auto & skip : skip_tb)
cout << skip << ", ";
cout << endl;
return skip_tb;
}
int search(const vector<int> bc_tb, const vector<int> gs_tb,
const string H, const string pattern)
{
const int h_size = H.size();
const int p_size = pattern.size();
int begin = 0;
if (h_size < p_size)
return -1;
while (begin <= h_size - p_size)
{
int matched = p_size;
while (matched > 0 && pattern[matched - 1] == H[begin + (matched - 1)])
{
--matched;
}
if (matched == 0)
return begin;
if (bc_tb[H[begin + matched]] != p_size)
{
begin += max(matched - bc_tb[H[begin + matched]],
gs_tb[matched]);
}
else
{
begin += max(gs_tb[matched], matched);
}
}
return -1;
}
int main()
{
const string h = "abaabaababbabababcabccaabcabcabcbcabcbacba";
const string pattern = "abbab";
const int p_size = pattern.size();
const vector<int> bc_table = make_to_bad_character_tb(pattern);
const vector<int> gs_table = make_to_gs_tb(pattern);
cout << search(bc_table, gs_table, h, pattern) << endl;
return 0;
}
with code & food :: [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (tistory.com)
'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [C#] 우선순위 큐 개념과 힙을 통한 구현 (0) | 2023.10.26 |
|---|---|
| 냅색 - meet in the middle (밋 인 더 미들) 알고리즘 (0) | 2023.10.25 |
| KMP (문자열 중 특정 패턴을 찾아내는 탐색) 알고리즘 C++ 구현 (0) | 2023.10.25 |
| 페이지 교체 알고리즘 (0) | 2023.10.23 |
| SPFA (Shortest Path Faster Algorithm) (0) | 2023.10.20 |
