개념
KMP 알고리즘은 문자열에서 특정 패턴을 효율적으로 찾을 수 있다. 살펴볼 문자열의 길이가 N, 찾고 싶은 패턴의 길이가 M이라면 O(N+M)의 시간 복잡도를 가지는 매우 효율적인 알고리즘이다.
KMP 알고리즘이 얼마나 효율적인지 알기 전에, 모든 문자열을 일일이 비교하는 경우를 살펴보자.
모든 문자열을 일일이 비교하는 경우(브루트 포스 : Brute Force)
"ABCDABCE"라는 문자열에서 "ABCE"라는 패턴을 찾는다고 해보자. 모든 문자열을 일일이 비교한 경우엔 아래와 같이
탐색을 진행할 것이다.
이처럼 모든 문자열을 비교하는 브루트 포스(Brute Force) 방식은 텍스트의 길이를 N, 찾고자 하는 패턴의 길이를 M이라고 했을 때 시간 복잡도가 O(NM)이다. 이는 매우 비효율적이다.


접두부 (Prefix)와 접미부(Postfix)
만약 찾고자 하는 패턴 문자열이 "ABCABCAC"라고 하자.
접두부는 문자열의 왼쪽에서부터 한 글자씩 추가되는 부분을,
접미부는 문자열의 오른쪽에서부터 한 글자씩 추가되는 부분을 뜻한다.

접두부는 A, AB, ABC... 이렇게 왼쪽부터 한 글자가 추가된다.
접미부는 C, AC, CAC... 이렇게 오른쪽부터 한 글자가 추가된다.
이때 접두부와 접미부는 전체 문자열은 될 수 없음을 주의하자.
실패 함수 ( failure function)와 실패 배열(int failure[])
실패 배열은 패턴의 각 인덱스까지 접두부와 접미부가 최대의 길이로 같을 때 접두부의 마지막 인덱스이다.
패턴 "ABCABCAC"의 실패 배열을 구한다고 하자.
1. failure[0] 구하기
failure[0]은 패턴의 인덱스 0까지 살펴봐야 한다. 즉, "A"에서 접두부와 접미부가 같은지 보자. 전체 문자열은 접두부와 접미부가 될 수 없다고 했으니 "A"에서는 접두부와 접미부가 같은 길이를 구할 수 없다. 이럴 때는 -1 값을 넣어 주면 된다.
참고로 failure[0] 은 무조건 -1일 수밖에 없다. 접두부와 접미부가 아예 존재할 수 없기 때문이다.
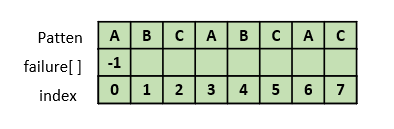
2. failure[1] 구하기
failure[1]은 패턴의 인덱스 1까지 살펴봐야 한다. "AB"에서도 접두부와 접미부가 같은 부분은 존재하지 않으므로 -1을 넣는다.
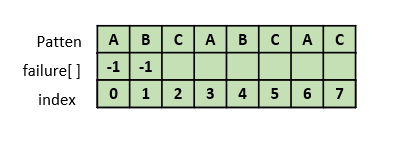
3. failure[2] 구하기
마찬가지로 "ABC"에서도 접두부와 접미부가 같은 부분은 존재하지 않으므로 -1을 넣는다.
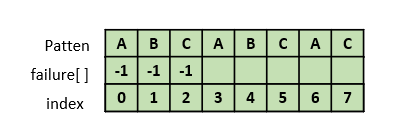
4. failure[3] 구하기
"ABCA"에서 "A"라는 접두부와 접미부가 같다. 이때 접두부와 접미부가 최대 길이로 같을 때의 접두부의 마지막 인덱스
는 0이다.
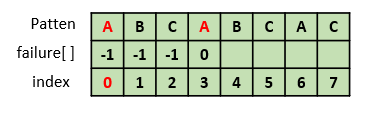
5. failure[4] 구하기
"ABCAB"에서 "AB"라는 접두부와 접미부가 같다. 이때 접두부와 접미부가 최대 길이로 같을 때의 접두부의 마지막 인덱스는 1이다.
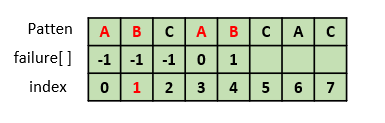
6. failure[5] 구하기
"ABCABC"에서 "ABC"라는 접두부와 접미부가 같다. 이때 접두부와 접미부가 최대 길이로 같을 때의 접두부의 마지막 인덱스는 2이다.
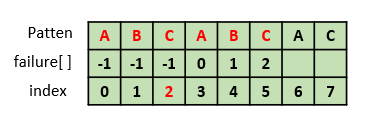
7. failure[6] 구하기
"ABCABCA"에서 "ABCA"라는 접두부와 접미부가 같다. 이때 접두부와 접미부가 최대 길이로 같을 때의 접두부의 마지막 인덱스는 3이다. ( 참고 : "A"도 접두부와 접미부가 같지만 최대 길이가 아니다)
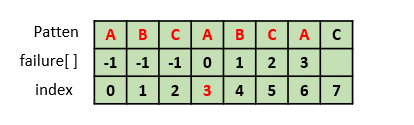
8. failure[7] 구하기
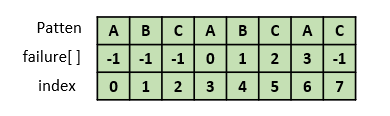
"ABCABCAC"에서 접두부와 접미부가 같은 부분은 존재하지 않으므로 -1을 넣는다.
헷갈린다면 모든 접두부와 접미부를 구해보자.
동작
미리 패턴에 대한 failure[] 배열을 만들어두었다고하자. KMP 알고리즘은 다음과 같은 과정을 거친다.
1. 본문과 패턴을 처음부터 비교한다.
2. 본문과 패턴을 비교해서 같다면 본문과 패턴 모두 한 글자씩 뒤로 계속 비교한다.
2-1. 만약 패턴의 첫 글자부터 다르다면 비교할 본문의 글자를 하나 미룬다.
2-2. 만약 패턴이 일치하는 부분이 있다면, 불일치하는 부분 직전까지의 failure[ ] 값 + 1부터 패턴을 다시 비교한다.
(비교할 본문의 글자는 그대로)
위 과정을 반복하면 된다.
"ABCABABCABCAC"라는 문자열에서 "ABCABCAC" 패턴을 찾는다고 하자.
이때 failure[ ] 배열의 정보를 이용하면 많은 부분을 건너뛸 수 있다.
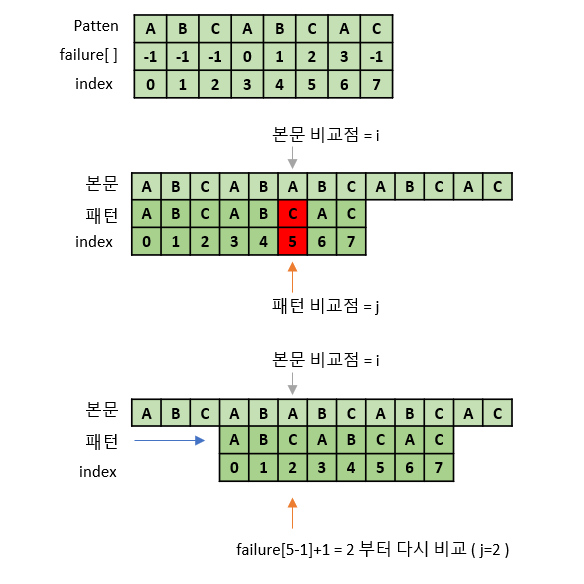
본문과 패턴이 "ABCAB"까지 일치하므로 본문 비교점 i와 패턴 비교점 j는 계속 한 칸씩 뒤로 간다.
그러다 패턴 5번 인덱스에서 불일치한다. 즉, 4번 인덱스까지는 일치한다는 뜻이다.
이때, failure[4] 배열에 담긴 값(=1)은 패턴의 4번 인덱스까지 고려했을 때 접두부와 접미부가 최대 길이로 같을 때 접두부의 마지막 인덱스이다. 즉, 본문과 일치하는 부분 "ABCAB"에서 접두부 "AB"와 접미부 "AB"가 같으므로 접두부를 접미부와 겹치게 밀어도 된다.
따라서 "AB"는 본문과 같다는 것을 이미 알기 때문에 접두부의 마지막 인덱스(=1) 바로 뒤(=2)부터 패턴과 본문을 다시 비교하면 되는 것이다.
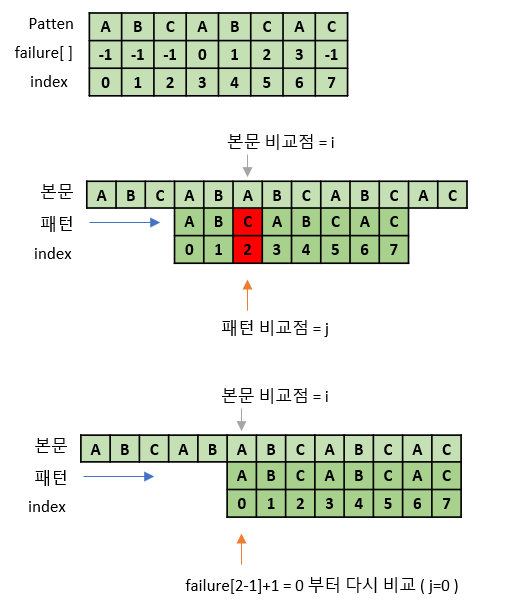
다시 본문과 패턴을 비교했을 때 "AB"까지 일치하다가 2번 인덱스에서 불일치한다.
따라서 패턴을 failure[2-1]+1 = 0 부터 다시 비교한다.
이제 본문에서 패턴을 찾았다.
이를 C++ 코드로 구현하면 다음과 같다.
int kmp(char* str, char* pat){
int i=0;
int j=0;
int lens = strlen(str);
int lenp = strlen(pat);
while(i<lens && j<lenp){
if(str[i] == pat[j]){ // 본문과 패턴이 같다면
i++; // 본문 한글자 뒤로
j++; // 패턴 한글자 뒤로
}else if(j==0){ // 패턴 첫글자부터 다르면
i++; // 본문 한글자 뒤로
}else{ // 같은 부분이 있다면
j = failure[j-1] + 1; // failure[] 배열 값 이용
}
}
return ( j == lenp ? i-lenp : -1); // 패턴이 일치할 경우 첫 인덱스 반환
}fail 함수
패턴에서 failure[ ] 배열을 구하는 fail 함수이다.
접두부와 접미부를 모두 브루트포스로 비교하는 것은 O(N^2)으로 비효율적이다.
이때 역시 KMP 알고리즘의 원리를 응용해서 failure[ ] 배열을 쉽게 구할 수 있다.
failure[ ] 배열을 이용해 failure[ ] 배열을 완성하는 것이다.
void fail(char *pat){
int j, n = strlen(pat);
failure[0] = -1; // failure[0] 는 무조건 -1
for(int i=1; i<n; i++){
j = failure[i-1];
while( (pat[i] != pat[j+1]) && (j>=0)){ // 일치할때까지
j = failure[j];
}
if( pat[i] == pat[j+1]){ // 일치하면
failure[i] = j+1;
}else{ // 일치하지 않으면
failure[i] = -1;
}
}
}패턴 "ABCABCAC"에서 failure[] 배열을 구한다고 하자.
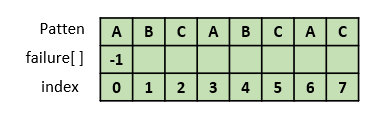
failure[0] 값은 무조건 -1이다. 한 글자는 접두부와 접미부가 없기 때문이다.
이후 i는 접미부, j는 접두부의 비교점이라고 하자.
j= failure[i-1]로 둘 수 있다. 왜냐하면 failure[i-1] 값이 i-1번째까지 접두부와 접미부가 최대 길이로 같을 때 접두부의 마지막 인덱스이기 때문이다. 따라서 그 뒤인 j+1 부터 비교를 시작하면 된다.
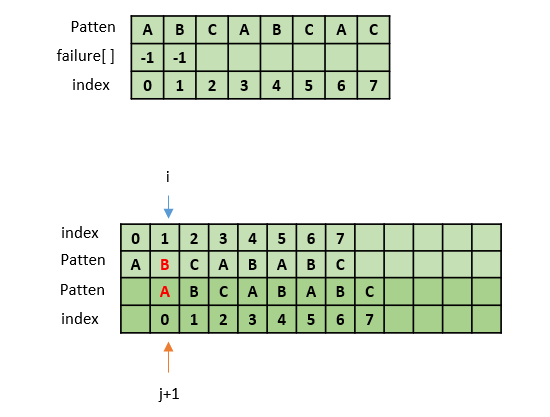
1. failure[1] 값 구하기
pat[1] 와 pat[0]이 일치하지 않으므로 failure[1] = -1이다.
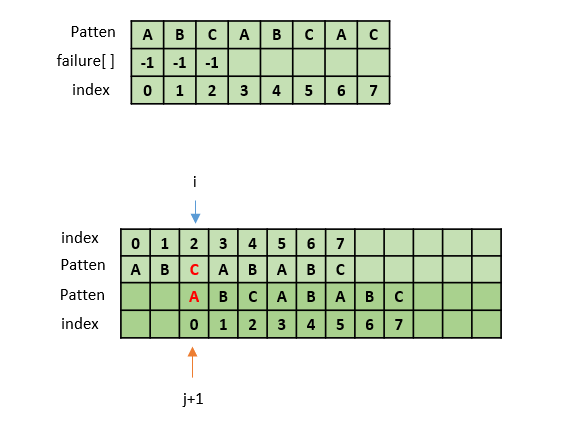
2. failure[2] 값 구하기
pat[2] 와 pat[0]이 일치하지 않으므로 failure[2] = -1이다.
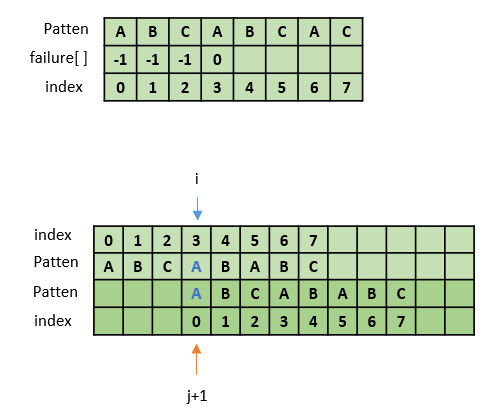
3. failure[3] 값 구하기
pat[3] 와 pat[0] 이 일치하므로 failure[3] = 0이다.
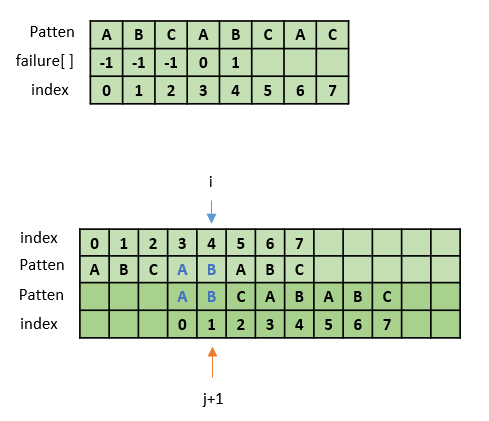
4. failure[4] 값 구하기
i = 4 일 때 다시 j+1 = 0부터 살펴볼 필요가 있을까? 그렇지 않다.
failure[4-1] = 0, 즉 "ABCA"에서 접두부와 접미부가 최대 길이로 같을 때 접두부의 마지막 인덱스는 0이므로
1부터 비교하면 된다. 따라서 failure[i-1] 보다 한 칸 뒤부터 살펴보면 된다.
따라서 j= failure[i-1]을 대입해 놓고 j+1부터 비교를 하는 것이다.
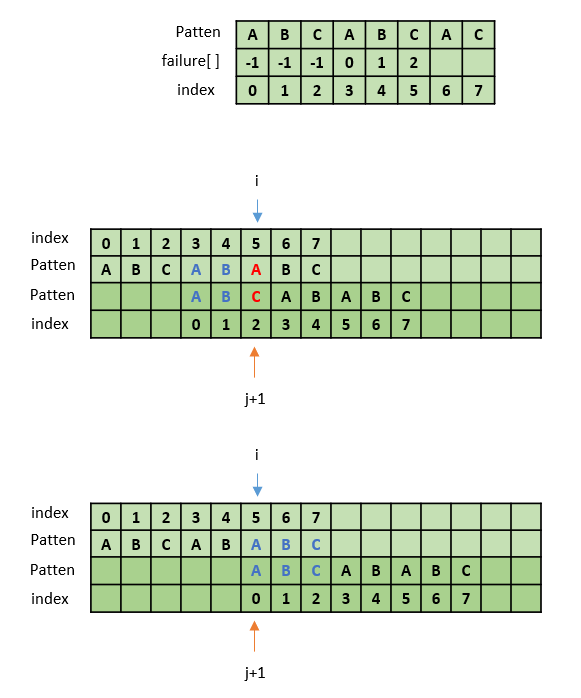
5. failure[5] 값 구하기
pat[i] 와 pat[j+1]이 불일치하면, j = failure[j]로 인덱스를 변경할 수 있다.
즉, 일치할 때까지 혹은 처음으로 접두부를 미는 것이다.
while( (pat[i] != pat[j+1]) && (j>=0)){ // 일치할때까지
j = failure[j];
}전체 코드
#include <iostream>
#include <string.h>
using namespace std;
int failure[10];
void fail(char *pat){
int j, n = strlen(pat);
failure[0] = -1; // failure[0] 는 무조건 -1
for(int i=1; i<n; i++){
j = failure[i-1];
while( (pat[i] != pat[j+1]) && (j>=0)){ // 일치할때까지
j = failure[j];
}
if( pat[i] == pat[j+1]){ // 일치하면
failure[i] = j+1;
}else{ // 일치하지 않으면
failure[i] = -1;
}
}
}
int kmp(char* str, char* pat){
int i=0;
int j=0;
int lens = strlen(str);
int lenp = strlen(pat);
while(i<lens && j<lenp){
if(str[i] == pat[j]){ // 본문과 패턴이 같다면
i++; // 본문 한글자 뒤로
j++; // 패턴 한글자 뒤로
}else if(j==0){ // 패턴 첫글자부터 다르면
i++; // 본문 한글자 뒤로
}else{ // 같은 부분이 있다면
j = failure[j-1] + 1; // failure[] 배열 값 이용
}
}
return ( j == lenp ? i-lenp : -1);
}
int main(){
char* str = "ABCABABCABCAC";
char* pat = "ABCABCAC";
fail(pat);
int result = kmp(str, pat);
if(result == -1){
cout << "패턴을 찾을 수 없습니" << endl;
}else{
cout << "인덱스 "<< result << " 부터 패턴입니다" << endl;
}
return 0;
}
'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| 냅색 - meet in the middle (밋 인 더 미들) 알고리즘 (0) | 2023.10.25 |
|---|---|
| Boyer-Moore (보이어무어) 알고리즘 / 문자열 탐색 (0) | 2023.10.25 |
| 페이지 교체 알고리즘 (0) | 2023.10.23 |
| SPFA (Shortest Path Faster Algorithm) (0) | 2023.10.20 |
| 알고리즘 대회 (Competitive Programming)에서 애드혹(Ad-Hoc) 문제란? (0) | 2023.10.20 |
