[DX11 물방울책] 챕터 7 - 광원

7.0 개념

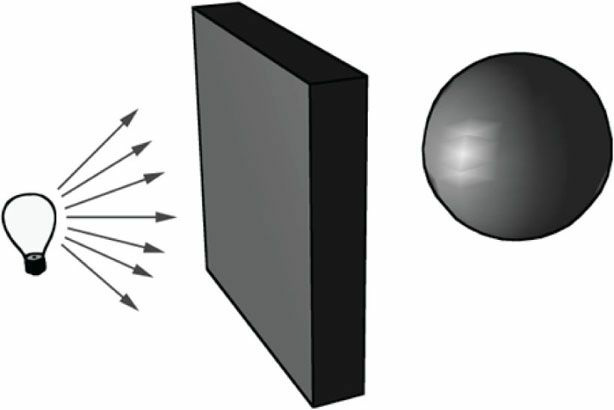
왼쪽 동그라미는 광원이 꺼져있어서 2D처럼 보인다 그에 반해 오른쪽 동그라미는 광원과 그림자가 추가되었기 때문에 3D처럼 인식된다.

 

이 모델에선 광원이 다양한 색상을 비추기 위해 rgb 색상 중 임의의 밝기로 조절할 수 있다. 빛이 어떠한 물체와 충돌 시 그 빛은 흡수 후 반사 되고 그렇게 소멸된다.

 

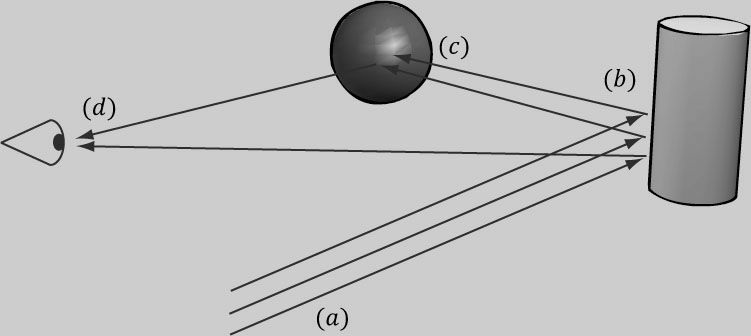
로컬 광원은 밝기의 중점이 물체에 있고, 각기 다른 밝기를 가지고있고 다른 물체와 독립적이다.

글로벌 광원은 각 물체의 밝기를 고려할 뿐만 아니라 전체 씬의 존재하는 오브젝트의 반사되는 빛 또한 고려한다. 상대적으로 비용이 매우 비싸며 이를 보완하기 위해 계속해서 연구 중에 있다.

7.2 단일 벡터

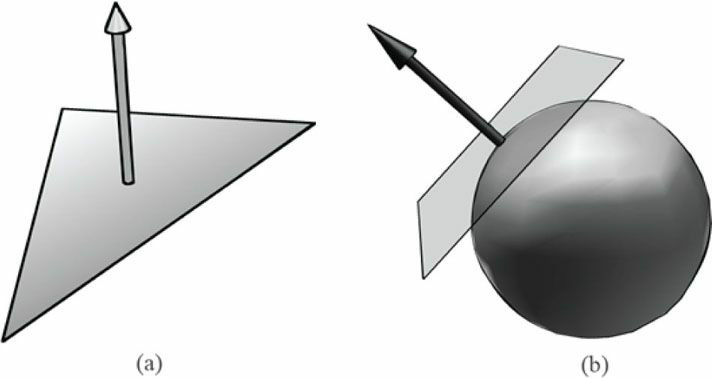
면이라는건 하나의 물체가 바라보고 있는 방향을 뜻한다.

표면이라는건 땅으로부터 바라보고 있는 방향을 뜻한다.

단일 벡터 n0와 n1은 p0와 p1로 인해 결정된다. 단일 벡터 n은 p와의 보간해서 얻는다. n = n0 + t (n1 – n0), t는 p = p0 + t (p1 – p0).

7.2.1 단일 벡터 계산하기

계산하기 위해서는 각 꼭지점들의 벡터 값을 알아야한다.

u = p1 – p0
v = p2 – p0

// 다음은 이를 찾는 함수

void ComputeNormal(const D3DXVECTOR3& p0,
const D3DXVECTOR3& p1,
const D3DXVECTOR3& p2,
D3DXVECTOR3& out)
{
D3DXVECTOR3 u = p1 - p0;
D3DXVECTOR3 v = p2 - p0;
D3DXVec3Cross(&out, &u, &v);
D3DXVec3Normalize(&out, &out);
}

다른 표면을 위해선 공통되는 점을 찾아낼 수 있지만 안타깝게도 삼각형은 이를 구분지을 수 없다 따라서 이걸 Vertex Normal Averaging 이라고 부른다. v의 버텍스 n은 v가 바라보고 있는 방향으로부터 구할 수 있다.

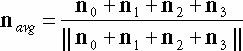
// Input:
// 1. An array of vertices (mVertices). Each vertex has a
// position component (pos) and a normal component (normal).
// 2. An array of indices (mIndices).
// For each triangle in the mesh:
for(UINT i = 0; i < mNumTriangles; ++i)
{
// indices of the ith triangle
UINT i0 = mIndices[i*3+0];
UINT i1 = mIndices[i*3+1];
UINT i2 = mIndices[i*3+2];
// vertices of ith triangle
Vertex v0 = mVertices[i0];
Vertex v1 = mVertices[i1];
Vertex v2 = mVertices[i2];
// compute face normal
Vector3 e0 = v1.pos - v0.pos;
Vector3 e1 = v2.pos - v0.pos;
Vector3 faceNormal = Cross(e0, e1);
// This triangle shares the following three vertices,
// so add this face normal into the average of these
// vertex normals.
mVertices[i0].normal += faceNormal;
mVertices[i1].normal += faceNormal;
mVertices[i2].normal += faceNormal;
}
// For each vertex v, we have summed the face normals of all
// the triangles that share v, so now we just need to normalize.
for(UINT i = 0; i < mNumVertices; ++i)
mVertices[i].normal = Normalize(&mVertices[i].normal));

7.2.2 단일 벡터 변환하기

(a) The surface normal before transformation. (b) After scaling by 2 units on the x-axis the normal is no longer orthogonal to the surface. (c) The surface normal correctly transformed by the inverse-transpose of the scaling transformation.

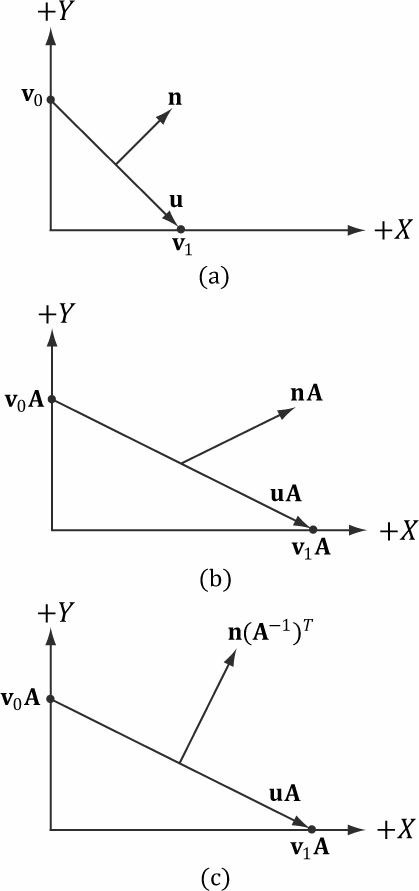
// 역 전치행렬

static XMMATRIX InverseTranspose(CXMMATRIX M)
{
XMMATRIX A = M;
A.r[3] = XMVectorSet(0.0f, 0.0f, 0.0f, 1.0f);
XMVECTOR det = XMMatrixDeterminant(A);
return XMMatrixTranspose(XMMatrixInverse(&det, A));
}

7.3 람버트 코사인 법칙

Figure 7.8. Consider a small area element dA. (a) The area dA receives the most light when the normal vector n and light vector L are aligned. (b) The area dA receives less light as the angle θ between n and L increases (as depicted by the light rays that miss the surface dA).

Plot of the function f (θ) = max (cos θ,0) = max (L · n, 0) for –2 ≤ θ ≤ 2. Note that π/2 ≈ 1.57.

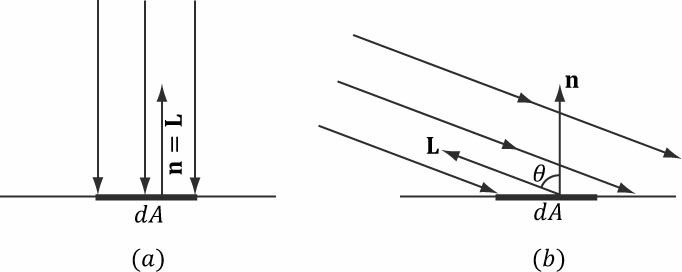
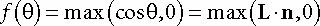
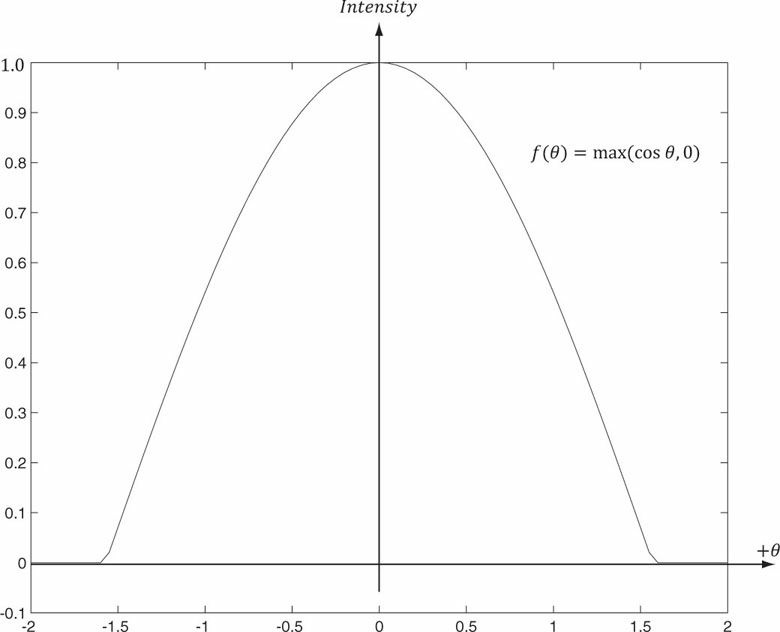
7.4 다방면으로 반사

공식) cd = kd · ιd ⊗ md = kd D

빛이 표면에 닿았을 시 여러 방향으로 반사

7.5 환경 광원

주변으로 흩어지는 빛의 대한 공식) A = ιa ⊗ ma

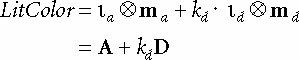
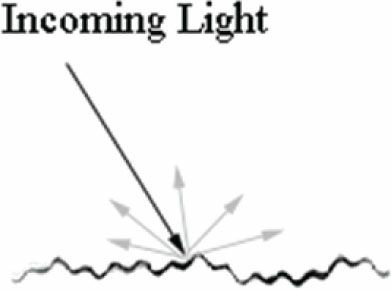
7.6 추측 광원

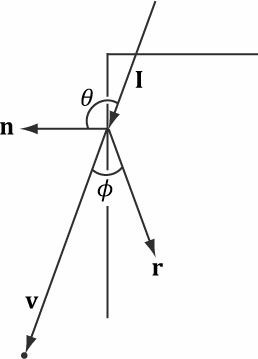
빛이 물체에 충돌했을 때 가느다랗게 꼬깔콘 모양의 추측되는 반사 경로를 통해 한 방향으로 반사된다.

공식

 

 

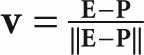
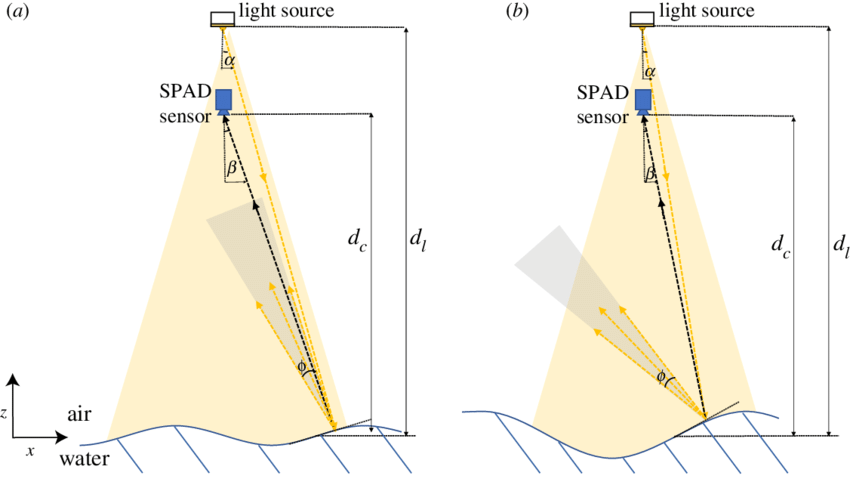
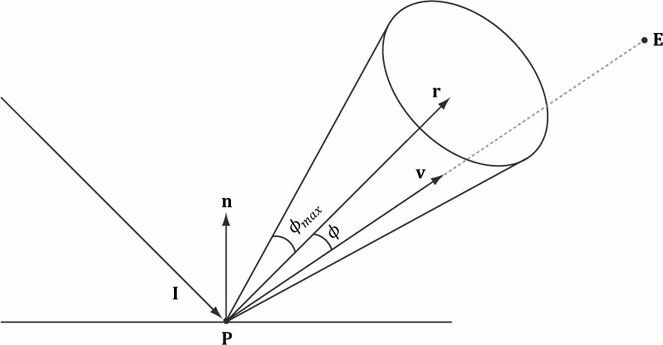
더 큰 면을 위해선

Plots of the cosine functions with different powers of p ≥ 1.

눈에게 비춰지는 빛의 양을 측정할려면

ls = 빛의 양

ms = 면에 비춰지는 추측되는 빛 값

ks = r와 v 사이의 각도 빛의 쎄기 / 면이 빛을 받지 않는다면 0

 

 

 

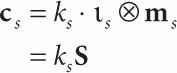
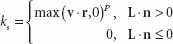
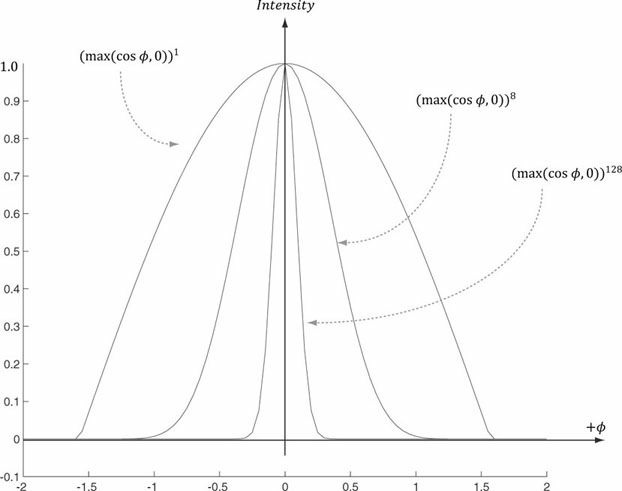
추정되는 빛의 힘 p는 1보다 항상 크거나 같아야한다

반사되는 도형

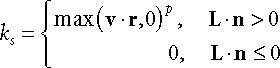
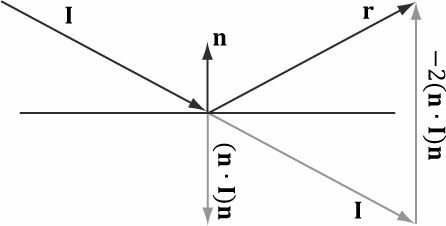
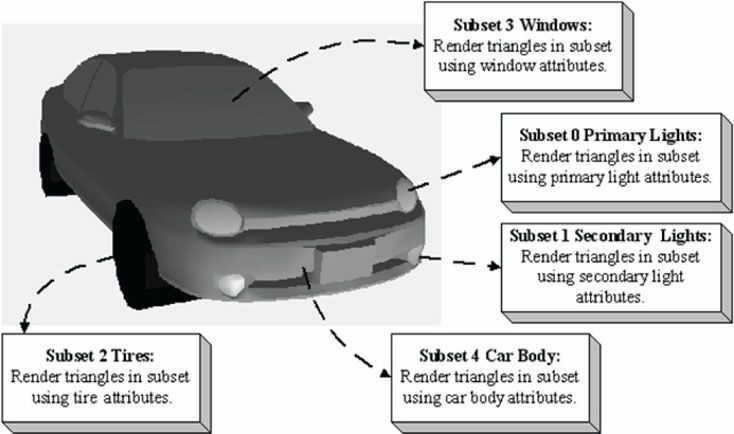
7.8 빛 반사되게끔 메터리얼 지정 방법

순서) 그리기 전 상수 버퍼에 넣어야함

주 빛 메터리얼 > 첫번째 도형 그림

주 빛 메터리얼 > 두번째 도형 그림

타이어 메터리얼 > 타이어 그림

유리 메터리얼 > 유리 그림

차체 메터리얼 > 차체 그림

struct Material
{
Material() { ZeroMemory(this, sizeof(this)); }
XMFLOAT4 Ambient;
XMFLOAT4 Diffuse;
XMFLOAT4 Specular; // w = SpecPower
XMFLOAT4 Reflect;
};

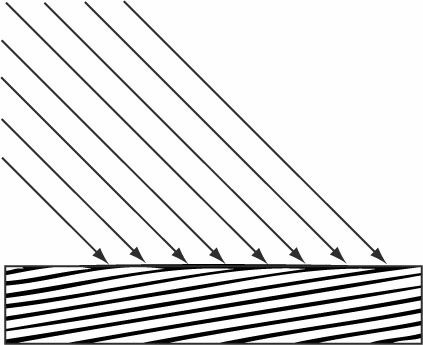
7.9 평행광

평행광은 아주 멀리 있는 빛을 추측해준다 그리고 이에 평행하는 모든 빛들 또한 추측할 수 있다. 당연히 같은 방향이므로 동일한 방향 벡터를 가지고 있다.

7.10 기점으로부터 빛

모든 방향으로 한 곳으로부터 빛이 발사된다.

 

방향에 따라 빛이 달라진다.

7.10.1 감쇠

빛이 멀어질 수록 밝기가 약해진다는건 당연한거다.

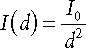
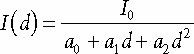
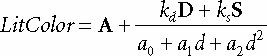
7.11 스포트라이트

스포트라이트는 마지막 지점에 꼬깔콘 형태로 원으로 비춘다.

 

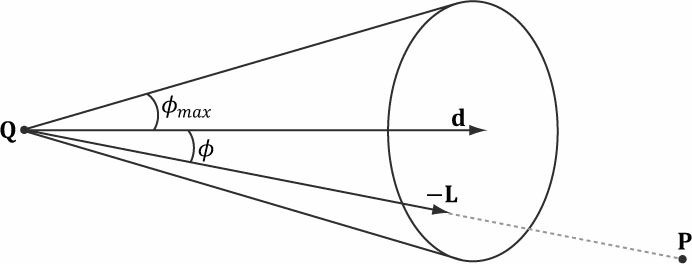
스포트라이트를 구현하기 위해선

P = 가리키고 있는 방향

Q = 스포트라이트의 위

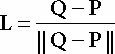
kspot (ϕ) = max (cosϕ,0)s = max (-L ·d, 0)s

 

스포트라이트에 대한 방정식은 기점으로 빛에 대한 방정식과 크게 다르진 않다.

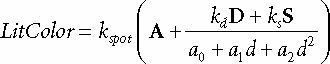
지형에 대한 수식

 

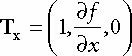
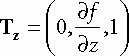
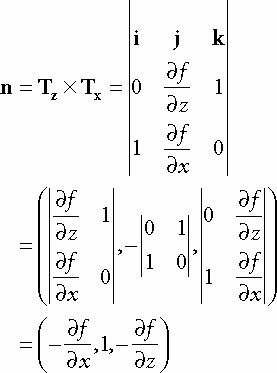
지형 메시를 생성하기 위해선

f (x, z) = 0.3 z · sin (0 . 1x) + 0 . 3x · cos (0 . 1z)

 

 

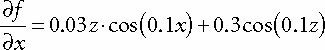
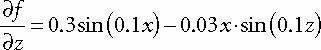
일반 지형은

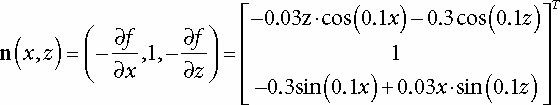
XMFLOAT3 LightingApp::GetHillNormal(float x, float z)const
{
// n = (-df/dx, 1, -df/dz)
XMFLOAT3 n(
-0.03f*z*cosf(0.1f*x) - 0.3f*cosf(0.1f*z),
1.0f,
-0.3f*sinf(0.1f*x) + 0.03f*x*sinf(0.1f*z));
XMVECTOR unitNormal = XMVector3Normalize(XMLoadFloat3(&n));
XMStoreFloat3(&n, unitNormal);
return n;
}