Principle of Locality
지역성에는 시간적 지역성과 공간적 지역성, 순차적 지역성이 있다.
- 시간적 지역성 : 최근에 액세스 된 프로그램이나 데이터가 가까운 미래에 다시 액세스 될 가능성이 높음을 의미한다. 반복루프, 서브루틴 호출, 공통 변수가 대표적인 예시다.
- 공간적 지역성 : 기억장치 내에 인접하여 저장된 데이터들이 연속적으로 액세스될 가능성이 높음을 의미한다. 표, 배열의 데이터가 그 대표적 예시다.
- 순차적 지역성 : 분기가 발생하지 않는 이상 명령어들이 기억장치에 저장된 순서대로 인출되어 실행됨을 의미한다. 이는 공간적 지역성에 편입되어 설명되기도 한다.

한 프로세스 안에도 자주 사용하는 부분과 그렇지 않은 부분이 있기 때문에 운영체제는 프로세스를 페이지(Page)라는 단위로 나눠 관리하며, 위 그림은 페이지를 참조한 기록이다. 가로 축은 실행 시간이고, 세로 축은 메모리 주소다. 즉, 수평으로 이어진 참조 기록은 긴 시간에 걸쳐 같은 메모리 주소를 참조한 것이고, 수직으로 이어진 참조 기록은 같은 시간에 밀접한 메모리 주소들을 참조한 것이다. 페이지에 접근할 때도 지역성 원리가 적용된다는 것을 알 수 있다.
Caches
+-------------+------+------+ +---------------+ +--------+
| | I$ | | <-- | | <-- | |
+ Processor +------+ L2 | | Main Memory | | Disk |
| | D$ | | --> | | --> | |
+-------------+------+------+ +---------------+ +--------+- L1 Cache: 프로세서와 가장 가까운 캐시. 속도를 위해 I$와 D$로 나뉜다.
- Instruction Cache (I$): 메모리의 TEXT 영역 데이터를 다루는 캐시.
- Data Cache (D$): TEXT 영역을 제외한 모든 데이터를 다루는 캐시.
- L2 Cache: 용량이 큰 캐시. 크기를 위해 L1 캐시처럼 나누지 않는다.
- L3 Cache: 멀티 코어 시스템에서 여러 코어가 공유하는 캐시.
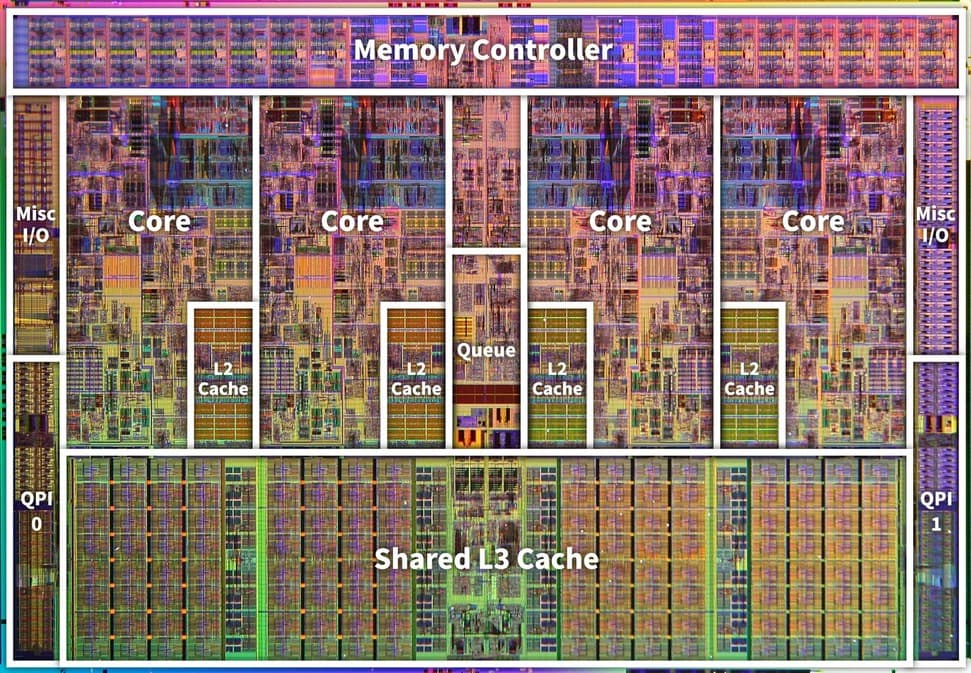
오늘날 CPU 칩의 면적 30~70%는 캐시가 차지한다. 1989년 생산된 싱글 코어 프로세서인 i486의 경우 8KB짜리 I/D 캐시 하나만 있었다. 한편 인텔 코어 i7 쿼드 코어 칩의 다이 맵(Die map)을 보면 4개의 코어에 각각 256KB L2 캐시가 있고, 모든 코어가 공유하는 8MB L3 캐시가 있는 것을 볼 수 있다. (L2 캐시 위에 있는 구역이 L1 캐시로 보이는데, 확실하지 않아서 따로 표시하지 않았다.)
Cache Metrics
캐시의 성능을 측정할 때는 히트 레이턴시(Hit latency)와 미스 레이턴시(Miss latency)가 중요한 요인으로 꼽힌다.
CPU에서 요청한 데이터가 캐시에 존재하는 경우를 캐시 히트(Hit)라고 한다. 히트 레이턴시는 히트가 발생해 캐싱된 데이터를 가져올 때 소요되는 시간을 의미한다. 반면 요청한 데이터가 캐시에 존재하지 않는 경우를 캐시 미스(Miss)라고 하며, 미스 레이턴시는 미스가 발생해 상위 캐시에서 데이터를 가져오거나(L1 캐시에 데이터가 없어서 L2 캐시에서 데이터를 찾는 경우) 메모리에서 데이터를 가져올 때 소요되는 시간을 말한다.
평균 접근 시간(Average access time)은 다음과 같이 구한다:

캐시의 성능을 높이기 위해서는 캐시의 크기를 줄여 히트 레이턴시를 줄이거나, 캐시의 크기를 늘려 미스 비율을 줄이거나, 더 빠른 캐시를 이용해 레이턴시를 줄이는 방법이 있다.
Cache Organization
캐시는 반응 속도가 빠른 SRAM(Static Random Access Memory)으로, 주소가 키(Key)로 주어지면 해당 공간에 즉시 접근할 수 있다. 이러한 특성은 DRAM(Dynamic Random Access Meomry)에서도 동일하지만 하드웨어 설계상 DRAM은 SRAM보다 느리다. 통상적으로 '메인 메모리’라고 말할 때는 DRAM을 의미한다.
주소가 키로 주어졌을 때 그 공간에 즉시 접근할 수 있다는 것은 캐시가 하드웨어로 구현한 해시 테이블(Hash table)과 같다는 의미다. 캐시가 빠른 이유는 자주 사용하는 데이터만을 담아두기 때문이기도 하지만, 해시 테이블의 시간 복잡도가 O(1) 정도로 빠르기 때문이기도 하다.
캐시는 블록(Block)으로 구성되어 있다. 각각의 블록은 데이터를 담고 있으며, 주소값을 키로써 접근할 수 있다. 블록의 개수(Blocks)와 블록의 크기(Block size)가 캐시의 크기를 결정한다.
Indexing
주소값 전체를 키로 사용하지는 않고, 그 일부만을 사용한다. 가령 블록 개수가 1024개이고, 블록 사이즈가 32바이트일 때, 32비트 주소가 주어진다면 다음과 같이 인덱싱 할 수 있다.
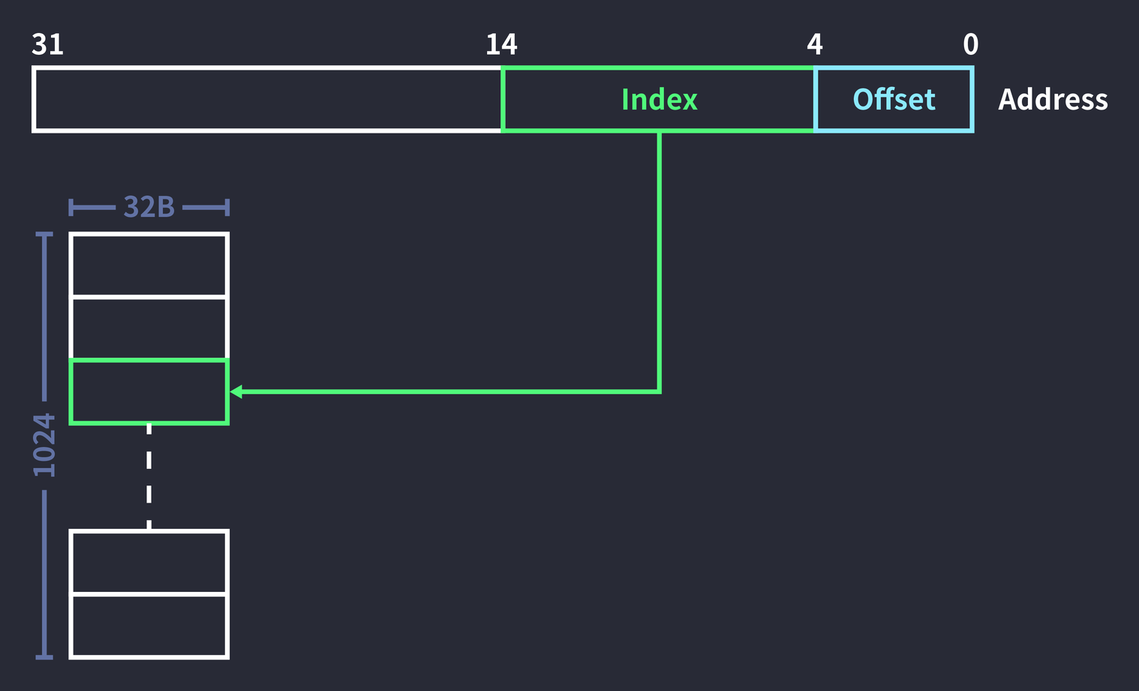
전체 주소에서 하위 5비트를 오프셋(Offset)으로 쓰고, 이후 10비트를 인덱스(Index)로 사용하여 블록에 접근했다. 인덱스가 10비트인 이유는 2^n개 블록의 모든 인덱스를 표현하기 위해서는 log{_2}\text{blocks}만큼의 비트가 필요하기 때문이다. 여기에선 블록 개수가 2^{10} = 1024개이므로, log{_2} 1024 = 10이 되어 10비트가 인덱스 비트로 사용되었다. (오프셋 비트에 대해서는 아래에서 설명하겠다.)
그러나 이렇게만 하면 서로 다른 데이터의 인덱스가 중복될 위험이 너무 크다.
Tag Matching
인덱스의 충돌을 줄이기 위해 주소값의 일부를 태그(Tag)로 사용한다. 블록 개수가 1024개이고, 블록 사이즈가 32바이트일 때, 32비트 주소 0x000c14B8에 접근한다고 가정해보자:
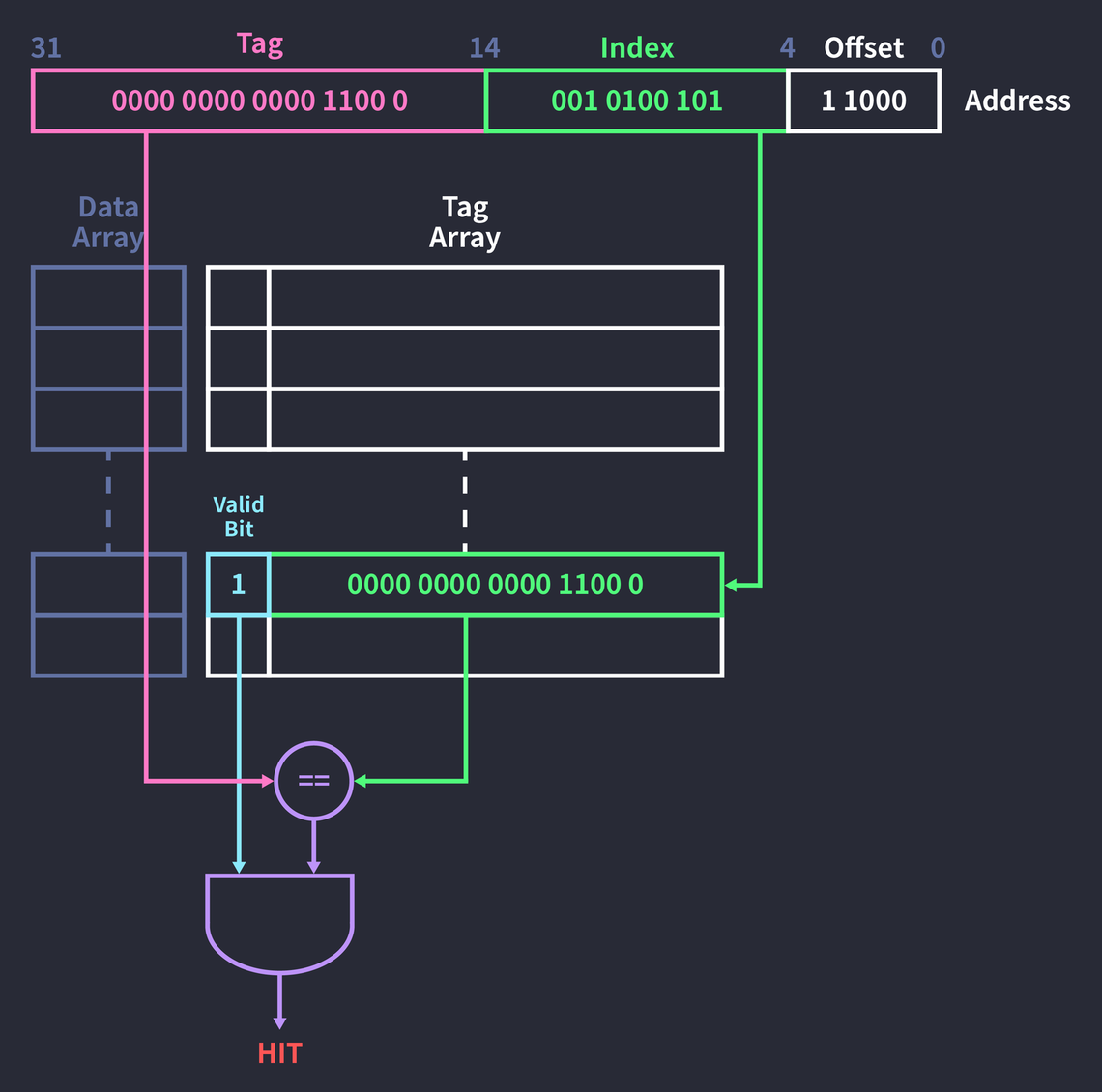
- 먼저 인덱스(0010100101)에 대응하는 태그 배열(Tag array)의 필드에 접근한다.
- 이어서 해당 태그 필드의 유효 비트(Valid bit)를 확인한다.
- 유효 비트가 1이라면 태그 필드(00000000000011000)와 주소의 태그(00000000000011000)가 같은지 비교한다.
- 비교 결과(true, 1)를 유효 비트(1)와 AND 연산한다.
유효 비트가 1이라는 것은 해당 블록에 올바른 값이 존재한다는 의미다. 태그 필드와 주소의 태그가 같고, 유효 비트도 1이므로 위 예시의 결과는 히트다. 히트가 발생하면 데이터 배열(Data array)에서 해당 인덱스의 데이터를 참조한다. (참고로 데이터 배열과 태그 배열도 모두 하드웨어다.)
만약 유효 비트가 0이라면 블록에 값이 없거나 올바르지 않다는 뜻이므로 미스가 발생한다. 그러면 주소의 태그를 태그 필드에 작성하고, 데이터 필드에도 상위 캐시나 메모리에서 요청한 값을 가져와 작성한 뒤, 유효 비트를 1로 바꿔준다.
유효 비트가 1이라도 태그가 일치하지 않으면 미스가 발생한다. 이 경우 교체 정책(Replacement policy)에 따라 처리가 달라진다. 먼저 입력된 데이터가 먼저 교체되는 FIFO(First-In First-Out) 정책을 사용한다면 무조건 기존 블록를 교체한다. 태그 배열의 필드를 주소의 태그로 바꾸고, 상위 캐시나 메모리에서 요청한 데이터를 가져와 데이터 필드의 값도 새 데이터로 바꿔준다. (실제로는 요청한 데이터뿐 아니라 그 주변 데이터까지 가져온다.) 기존 데이터는 상위 캐시로 밀려난다.
주소의 상위 15비트가 태그 비트로 사용된 이유는 태그 비트가 \text{Address bits} - (\log{_2}\text{Block size} + \text{Index bits})로 결정되기 때문이다. 이 경우 32 - (5 + 10) = 17 비트가 태그 비트로 사용되었고, 남은 5비트는 오프셋 비트로 사용되었다.
Tag Overhead
태그 배열이 추가되면서 더 많은 공간이 필요하게 되었다. 하지만 여전히 '32KB 캐시’는 32KB 데이터를 저장할 수 있는 캐시라는 의미다. 태그를 위한 공간은 블록 크기와 상관없는 오버헤드(Overhead)로 취급하기 때문이다.
1024개의 32B 블록으로 구성된 32KB 캐시의 태그 오버헤드를 구해보자:
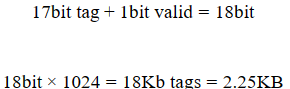
즉, 7%의 태그 오버헤드가 발생했다.
공간뿐 아니라 시간 비용도 발생한다. 태그 배열에 접근해 히트를 확인하고, 그 이후에 데이터 배열에 접근해 데이터를 가져오기 때문에 결과적으로 히트 레이턴시가 증가하게 된다.
그래서 두 과정을 병렬적으로 실행한다. 태그 배열에서 히트 여부를 확인하는 동시에 미리 데이터 배열에 접근하는 것이다. 이렇게 하면 히트 레이턴시가 줄어들지만, 미스가 발생했을 때의 리소스 낭비를 감수해야 한다.
Associative Cache
서로 다른 두 주소가 같은 인덱스를 가지면 충돌이 발생하고, 교체 정책에 따라 블록을 교체한다. 하지만 충돌이 발생할 때마다 캐시 내용을 바꾸면 더 많은 미스가 발생하게 되고, 한 자리의 내용을 끝없이 바꾸는 핑퐁 문제(Ping-pong problem)가 일어날 수 있다.
이 문제는 태그 배열과 데이터 배열을 여러 개 만드는 식으로 개선할 수 있다. 즉, 인덱스가 가리키는 블록이 여러 개가 되는 것이다. 인덱스가 가리키는 블록의 개수에 따라 캐시의 종류를 분류하면 아래와 같다:
- Direct mapped: 인덱스가 가리키는 공간이 하나인 경우. 처리가 빠르지만 충돌 발생이 잦다.
- Fully associative: 인덱스가 모든 공간을 가리키는 경우. 충돌이 적지만 모든 블록을 탐색해야 해서 속도가 느리다.
- Set associative: 인덱스가 가리키는 공간이 두 개 이상인 경우. n-way set associative 캐시라고 부른다.
direct mapped 캐시와 fully associative 캐시 모두 장단점이 극단적이기 때문에 보통은 set associative 캐시를 사용한다.
Set Associative Cache Organization
간단하게 2-way set associative 캐시의 동작을 살펴보자:
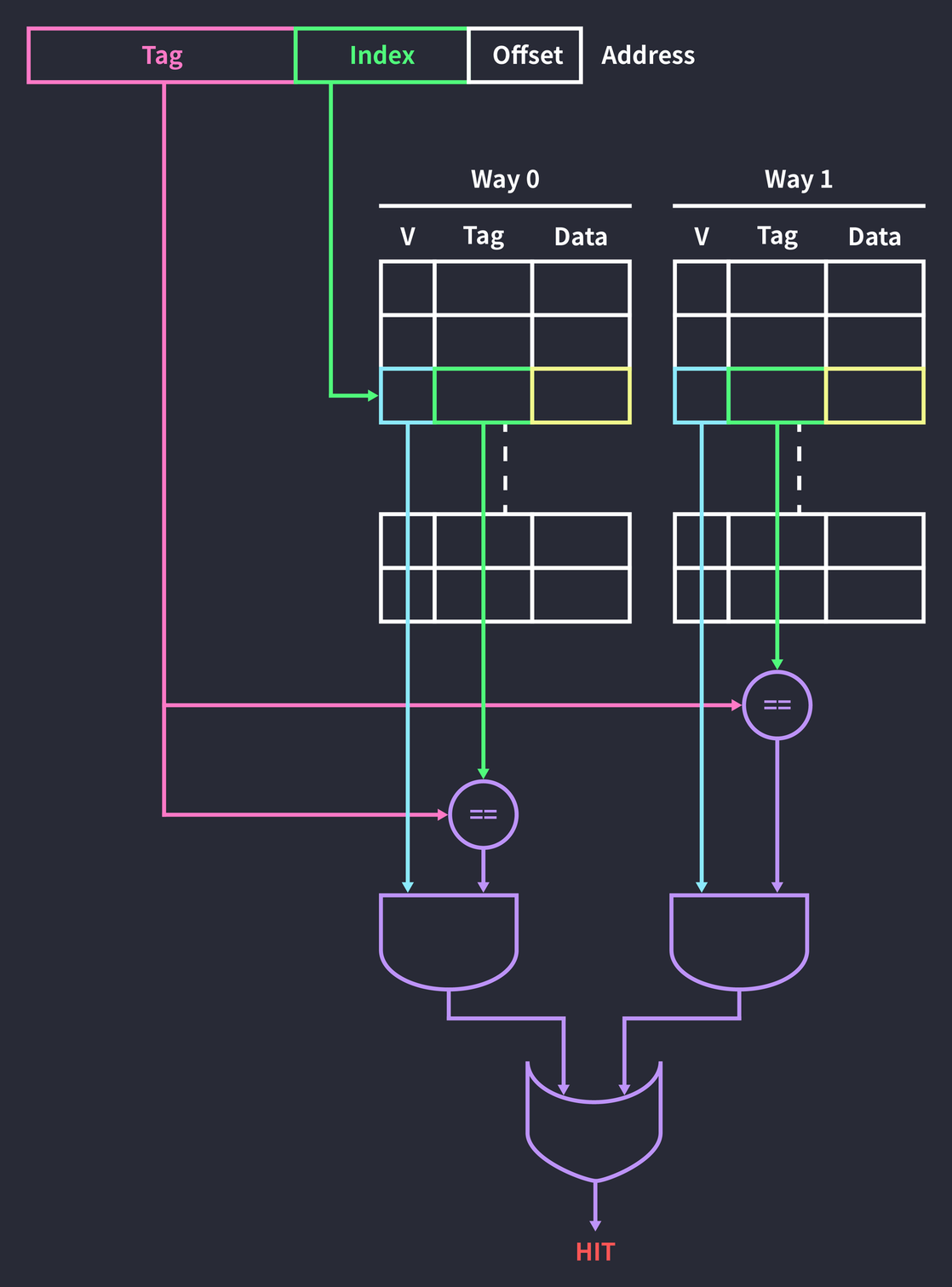
주소의 인덱스를 통해 블록에 접근하는 것은 지금까지 본 direct mapped 캐시와 동일하다. 다만 2개의 웨이(Way)가 있기 때문에 데이터가 캐싱되어 있는지 확인하려면 하나의 블록만이 아닌 2개의 블록을 모두 확인해야 한다. 마지막으로 두 웨이의 결과를 OR 연산하면 최종 결과를 낼 수 있다. 모든 웨이에서 미스가 발생하면 교체 정책에 따라 2개의 블록 중 한 곳에 데이터를 작성한다.
direct mapped 캐시와 비교해서 히트 레이턴시를 높이는 대신 충돌 가능성을 줄인 것이다.
Concrete Example
2바이트 캐시 블록으로 구성된 8바이트 2-way 캐시가 있고, 4비트 주소가 주어진다고 가정해보자.
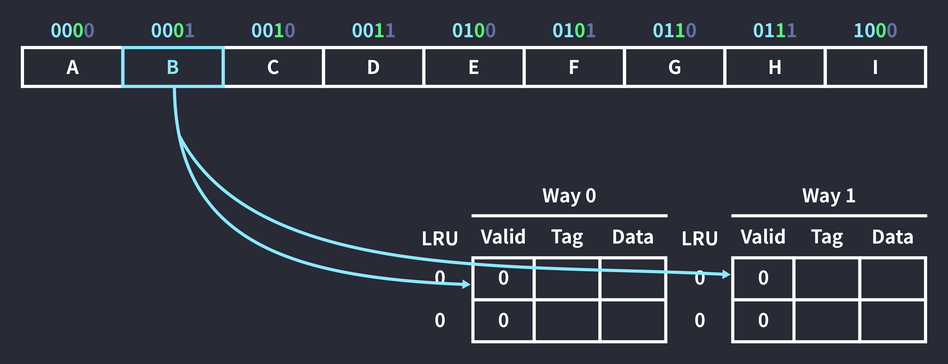
메모리 주소 0001을 참조하는 명령이 실행되었다. 인덱스 비트는 \log{_2} 2 = 1이고, 태그 비트는 4 - (log{_2} 2 + 1) = 2이다. 마지막으로 오프셋 비트는 1이 된다. 따라서 주소 0001의 인덱스는 0, 태그는 00이다. 즉, 해당 메모리 공간에 위치한 데이터는 인덱스가 0인 두 공간 중 한 곳에 캐싱될 수 있다.
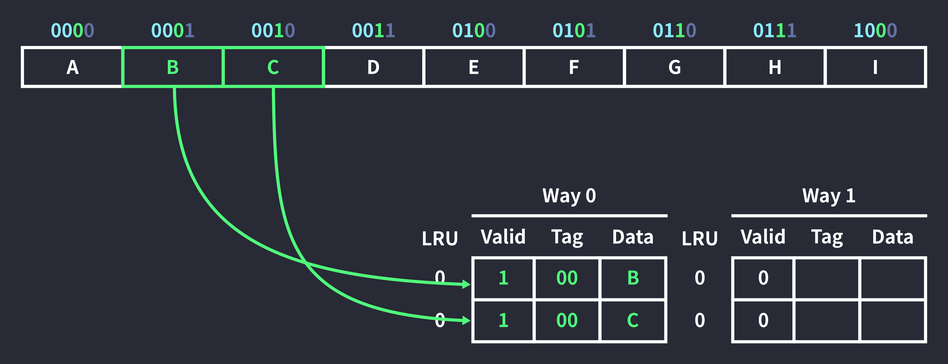
Way 0의 블록이 비어있으므로 Way 0에서 인덱스가 0인 블록에 데이터를 저장했다. 이때 주소 0010도 같이 캐싱되었는데, 이는 캐시 히트 비율을 높이기 위해 메모리에서 한 번에 캐시 블록 크기(2B)만큼 데이터를 가져오기 때문이다. (공간 지역성을 활용한 것이다.) 여기서는 참조한 데이터(0001)의 주변 공간인 0010을 함께 캐싱했다.
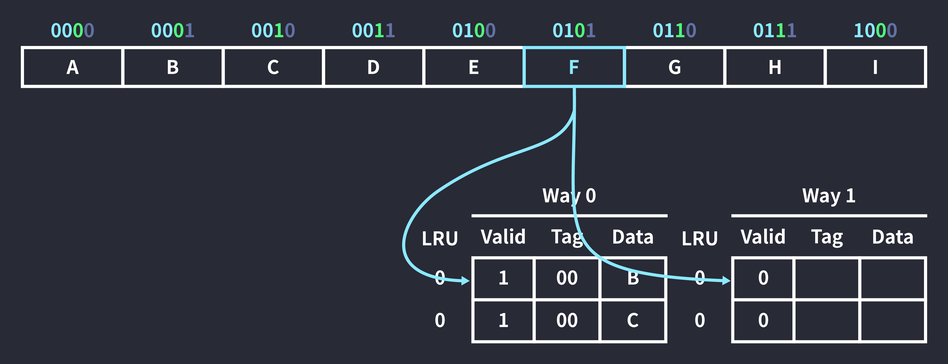
메모리 주소 0101을 참조하는 명령이 실행되었다. 이번에도 인덱스가 0인 두 공간에 들어갈 수 있다.
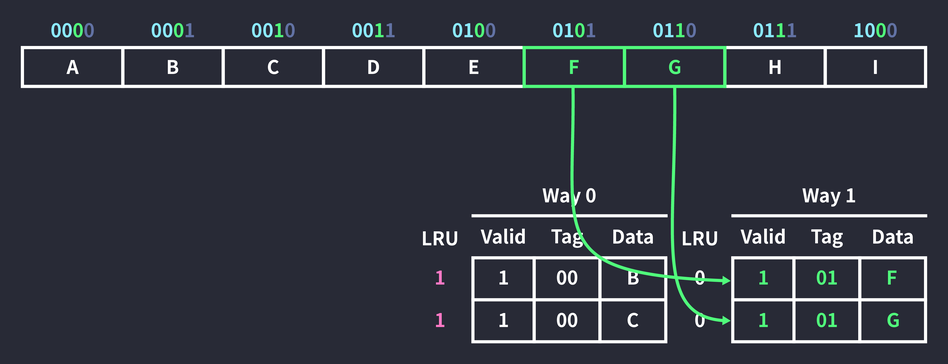
하지만 Way 0에서 인덱스가 0인 블록은 이미 데이터를 가지고 있기 때문에 데이터가 없는 Way 1에 캐싱된다. 이번에도 옆에 있는 0110 데이터가 함께 캐싱되었다. 또한 Way 0에 속한 두 블록의 LRU(Least Recently Used) 값이 증가했다. LRU는 사용한지 더 오래된 데이터를 우선적으로 교체하는 정책으로, 운영체제의 프로세스 스케줄링이나 페이지 교체 알고리즘으로도 사용된다. LRU 값이 증가했다는 것은 캐시 미스가 발생했을 때 우선적으로 교체될 가능성이 높아졌다는 의미다.
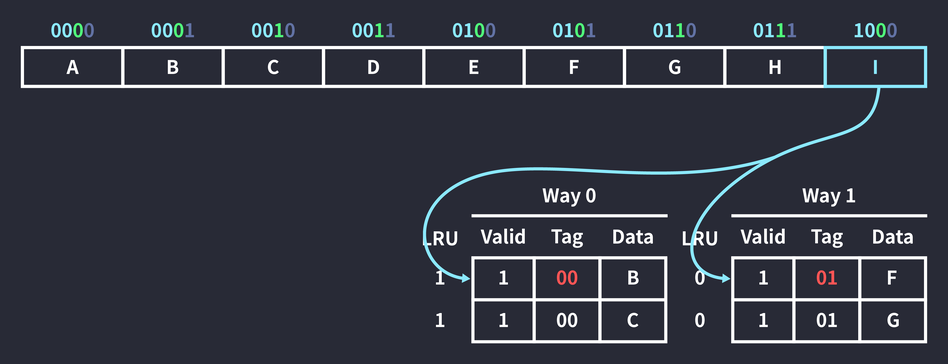
이어서 메모리 주소 1000을 참조하는 명령이 실행되었다. 인덱스가 0인 두 블록을 확인했으나, 태그가 10인 데이터가 없어 캐스 미스가 발생했다.
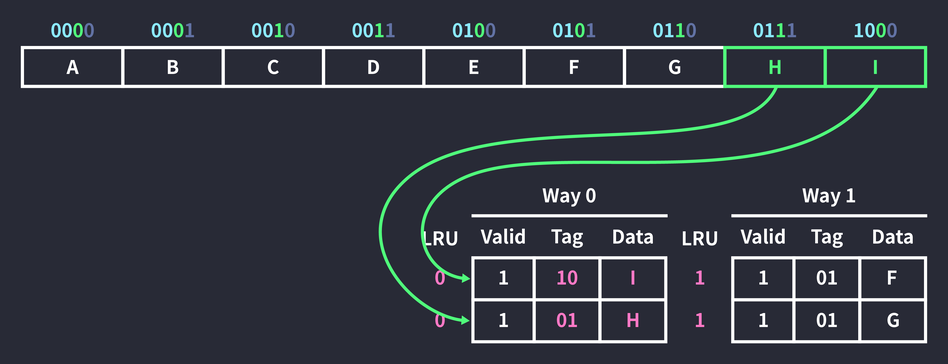
결국 캐싱된 데이터를 교체한다. 두 공간 중 Way 0 블록의 LRU 값이 더 크기 때문에 Way 0의 첫 번째 블록이 교체 되었고, 참조가 일어났으므로 LRU 값을 0으로 초기화했다. (캐시 히트가 발생하는 경우에도 LRU 값을 초기화한다.) 참조한 데이터의 주변 공간인 0111의 데이터도 같은 원리로 캐싱했다. 이때 Way 1에 속한 두 블록은 참조되지 않았기 때문에 LRU 값이 증가했다.
Handling Cache Writes
데이터를 읽는 동작이 아니라 입력하는 동작이 발생하고, 데이터를 변경할 주소가 캐싱된 상태(Write hit)라면 메모리의 데이터가 업데이트되는 대신 캐시 블록의 데이터가 업데이트된다. 이제 '캐시에서 업데이트된 데이터를 언제 메모리에 쓸 것인가?'에 관한 문제가 생긴다. 여기 두 가지 쓰기 정책(Write policies)이 있다.
하나는 Write-through 방식이다. 캐시에 데이터가 작성될 때마다 메모리의 데이터를 업데이트하는 것이다. 이렇게 하면 많은 트래픽이 발생하지만, 메모리와 캐시의 데이터를 동일하게 유지할 수 있다.
또 다른 방식은 Write-back 방식이다. 이 방식은 블록이 교체될 때만 메모리의 데이터를 업데이트한다. 데이터가 변경됐는지 확인하기 위해 캐시 블록마다 dirty 비트를 추가해야 하며, 데이터가 변경되었다면 1로 바꿔준다. 이후 해당 블록이 교체될 때 dirty 비트가 1이라면 메모리의 데이터를 변경하는 것이다.
데이터를 변경할 주소가 캐싱된 상태가 아니라면(Write miss) Write-allocate 방식을 사용한다. 당연한 얘기지만, 미스가 발생하면 해당 데이터를 캐싱하는 것이다. write-allocate를 하지 않는다면 당장은 리소스를 아낄 수 있겠지만 캐시의 목적을 달성하지는 못할 것이다.
Software Restructuring
여기까지 로우 레벨에서의 캐시 구조와 동작을 살펴봤는데, 코드 레벨에서 캐시의 효율을 증가시킬 수도 있다. 다음 이중 루프를 보자:
for (i = 0; i < columns; i += 1) {
for (j = 0; j < rows; j += 1) {
arr[j][i] = pow(arr[j][i]);
}
}2차원 배열의 모든 요소를 제곱하는 루프다. 큰 문제가 없어보이지만 공간 지역성을 따져보면 비효율적인 코드다. 배열 arr의 요소들은 메모리에 연속적으로 저장되는데, 접근은 순차적으로 이뤄지지 않기 때문이다.
0 4 8 12 16 20 24
+----------+----------+----------+----------+----------+----------+
| [0, 0] | [0, 1] | [0, 2] | [1, 0] | [1, 1] | [1, 2] |
+----------+----------+----------+----------+----------+----------+- i = 0, j = 0: 첫 번째 공간 [0, 0]에 접근한다.
- i = 0, j = 1: 네 번째 공간 [1, 0]에 접근한다.
- i = 1, j = 0: 두 번째 공간 [0, 1]에 접근한다.
이처럼 공간을 마구 건너뛰며 접근하게 된다. 따라서 아래 코드처럼 외부 루프는 rows를, 내부 루프는 columns를 순회해야 한다.
for (i = 0; i < rows; i += 1) {
for (j = 0; j < columns; j += 1) {
arr[i][j] = pow(arr[i][j]);
}
}비슷하지만 시간 지역성을 활용하는 예시도 있다. 다음 루프를 보자:
for (i = 0; i < n; i += 1) {
for (j = 0; j < len; j += 1) {
arr[j] = pow(arr[j]);
}
}배열 arr의 모든 요소를 제곱하는 동작을 n회 반복하는 이중 루프다. 현재 코드는 데이터를 캐싱한 뒤, 다음 접근 때 캐싱한 데이터에 접근한다는 보장이 없다. 전체 데이터가 캐시 크기보다 크다면 배열을 순회하는 과정은 아래 그림과 같을 것이다.
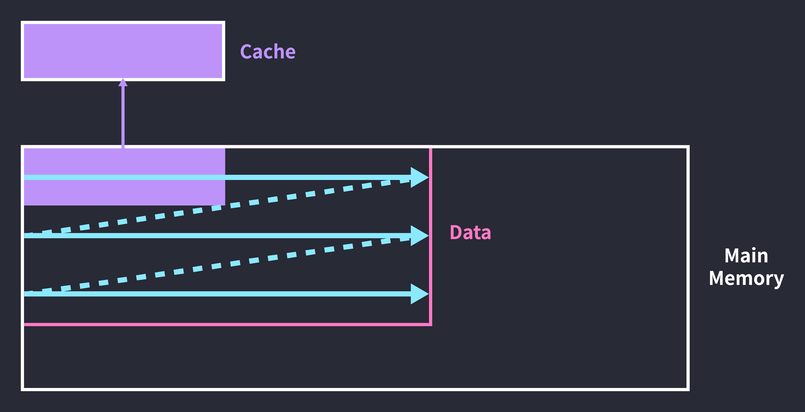
루프의 전반부에서 데이터를 캐싱하지만, 루프가 끝날 때 캐시는 후반부에 접근한 데이터로 덮어씌워진 상태가 된다. 그래서 두 번째 루프를 돌 때는 전반부 데이터를 다시 캐싱해야 한다. 캐싱한 데이터에 다시 접근하기도 전에 캐시 블록 전체가 교체되어 버리는 것이다. 배열 순회 주기를 캐시 크기만큼 끊어주면 문제를 해결할 수 있다.
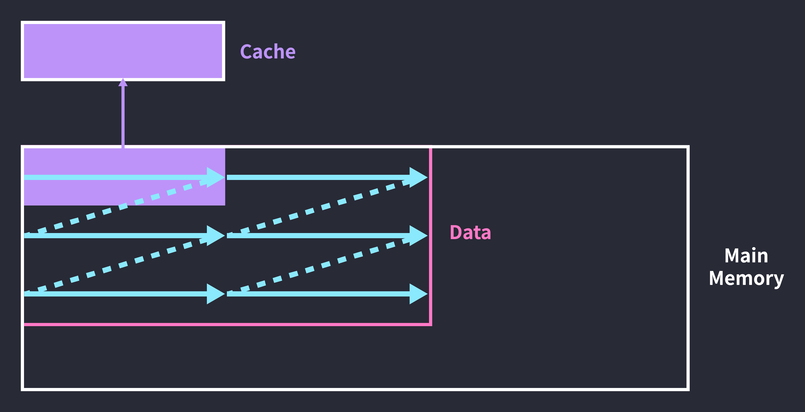
루프를 도는 횟수는 늘었지만 캐시 히트 비율은 더 높아졌다. 세 번째 루프까지는 전반부 데이터만 처리하고, 그 이후로는 후반부 데이터만 처리하는 것이다. 코드로 구현하면 삼중루프(!)가 된다:
for (i = 0; i < len; i += CACHE_SIZE) {
for (j = 0; j < n; j += 1) {
for (k = 0; k < CACHE_SIZE; k += 1) {
arr[i + k] = pow(arr[i + k]);
}
}
}'CS > OS & 하드웨어' 카테고리의 다른 글
| PCB(Process Control Block)란? (0) | 2022.12.28 |
|---|---|
| 문맥 교환 Context Switching (0) | 2022.12.27 |
| 캐시 히트율/메모리 적중률 (Hit Rate) (0) | 2022.12.26 |
| 페이징(Paging)이란? 페이지 테이블이란? (0) | 2022.12.16 |
| 바이오스 (BIOS - Basic Input/Output System) (0) | 2022.11.13 |
