개념
어떤 임의의 수열이 주어졌을 때, 수열에서 앞에서부터 차례대로 몇 개의 숫자들을 뽑아서 부분수열을 만들 수 있다. 이렇게 만들 수 있는 부분수열 중 오름차순으로 정렬된 가장 긴 수열을 최장 증가 부분 수열(LIS, Longest Increasing Subsequence)라고 한다.
예를 들어 [5, 2, 1, 4, 3, 5] 라는 수열이 있다고 가정해보자. 해당 수열에서 최장 증가 부분 수열에 해당하는 수열은 무엇일까?
- 세번째에 있는 숫자 1을 꺼낸다.
- 다섯번째에 있는 숫자 3을 꺼낸다.
- 여섯번째에 있는 숫자 5를 꺼낸다.
이렇게 만들어진 수열 [1, 3, 5]가 위 수열에서 만들 수 있는 최장 증가 부분 수열에 해당하고 길이는 3이 된다.
구할 수 있는 방법에는 크게 2가지가 있고 시간 복잡도에서 차이가 있다.
- Dynamic Programming (동적 계획법)
- Binary Search (이분 탐색)
1. DP 사용
dp를 이용한 방법은 O(N^2)의 시간이 걸린다. 이 방법은 입력 받은 배열의 숫자를 하나씩 살펴보며 이를 통해 LIS의 길이를 구하는 방법이다. 위의 예제의 수열을 사용하여 이 과정을 살펴 보자.
먼저 dp[0]은 위와 같이 1로 초기화 해준다. 증가 부분 수열의 길이는 1부터 시작한다.

다음으로 array[1]을 살펴보자. 앞의 array의 값과 비교했을 때 작으므로 dp[1]에는 1이 들어간다.

array[2] 역시 앞의 array 값들과 비교했을 때 작으므로 dp[2]에는 1이 들어간다.

array[3]은 array[1]과 array[2]에 비해 큰 값이다. dp[1]과 dp[2]는 값이 1로 같으므로 dp[3]에는 1 + 1인 2가 들어가게 된다.
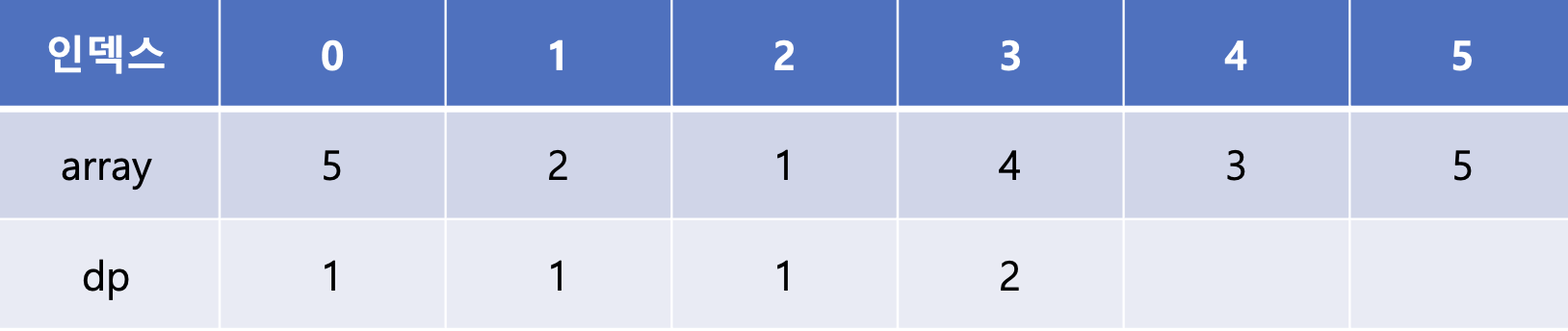
array[4]는 array[1]과 array[2]에 비해 큰 값이다. dp[1]과 dp[2]는 값이 1로 같으므로 dp[3]에는 1 + 1인 2가 들어가게 된다.
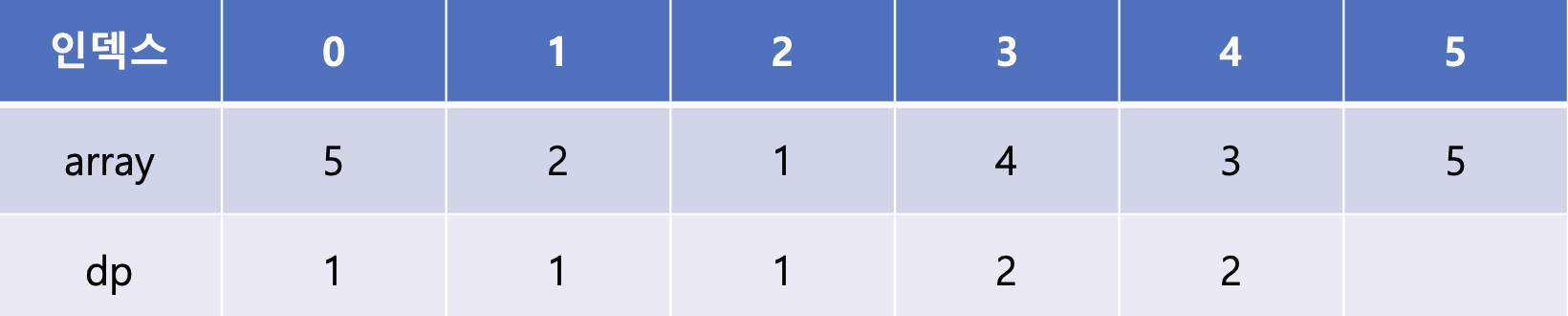
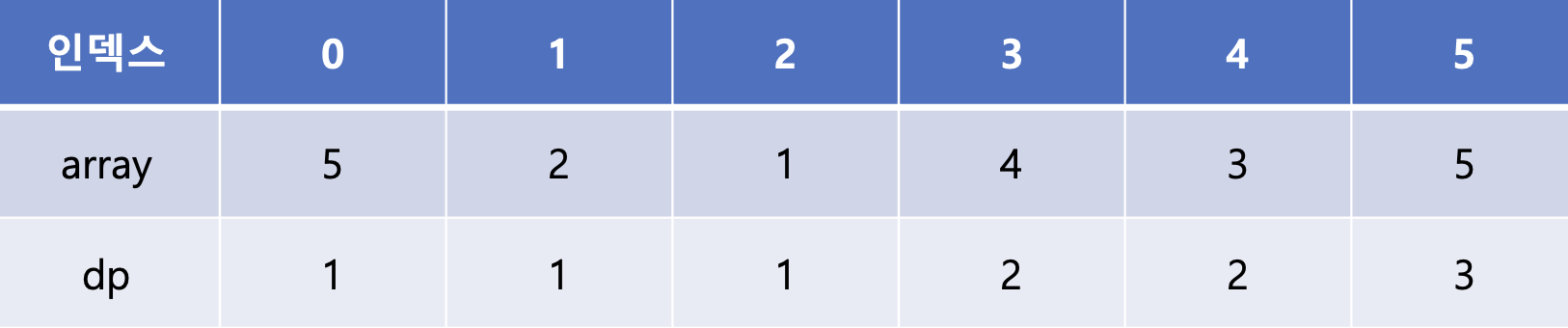
마지막 array[5]는 array[1], array[2], array[3], array[4]에 비해 큰 값이다. 이 중 dp[3]과 dp[4]가 2로 가장 큰 값이므로 dp[5]에는 2 + 1인 3이 들어가게 된다. 이렇게 만들 수 있는 모든 부분 증가 수열의 길이를 구하였고 이중 LIS의 길이는 dp배열에서 가장 큰 값에 해당하는 3에 해당된다.
코드
#include <iostream>
#include <vector>
using namespace std;
vector<int> v{ 5, 2, 1, 4, 3, 5 };
vector<int> dp(v.size());
void LIS_DP()
{
for (int i = 0; i < v.size(); i++)
{
dp[i] = 1; //해당 원소에서 끝나는 LIS 길이의 최솟값. 즉, 자기 자신
for (int j = 0; j < i; j++)
{
//i번째 이전의 모든 원소에 대해, 그 원소에서 끝나는 LIS의 길이를 확인한다.
if (v[i] > v[j])
{
//단, 이는 현재 수가 그 원소보다 클 때만 확인한다.
dp[i] = max(dp[i], dp[j] + 1); //dp[j] + 1 : 이전 원소에서 끝나는 LIS에 현재 수를 붙인 새 LIS 길이
}
}
}
}2. Binary Search 사용
dp를 사용한 LIS를 구하기 위해서는 수열의 값을 하나씩 비교해가며 길이를 구하기 때문에 O(N^2)의 시간이 걸리게 된다. 하지만 이분탐색을 사용하면 모든 수열의 값을 일일이 비교하지 않고 LIS의 길이를 구할 수 있기 때문에 O(N log N)의 시간으로 해결할 수 있다.
이를 위해 배열은 dp와 x 총 2가지가 사용된다. dp는 위와 같이 증가 부분 수열의 길이를 저장해 놓는 배열이고 x는 해당 부분 수열의 값들을 저장해 놓는 배열로 증가 부분 수열의 길이가 n일 때,
위의 예제를 이분 탐색을 사용하여 LIS의 길이를 구해보자. 처음에는 dp[0]에 1을 넣어주고 x[0]에는 array의 첫 번째 값인 5를 넣어준다.
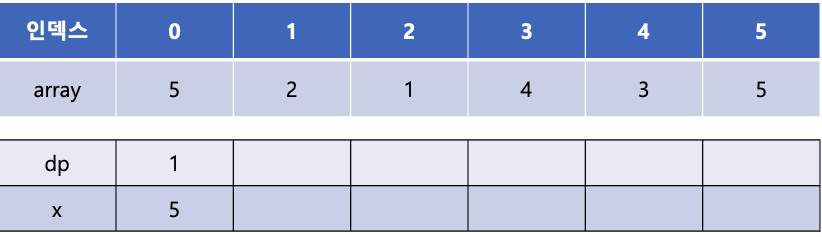
이제 array[1]의 값이 x 배열에서 어디에 들어갈 수 있는지를 이분탐색을 통해 찾는다. 2는 x 배열의 0번째 인덱스에 들어갈 수 있으며 x[0]에 있는 5보다 작다. 이렇게 해당 인덱스에 있는 x 배열의 값보다 현재 값이 작을 경우에는 x 배열의 값을 갱신해 준다. 즉, 위에서는 x[0]에 5대신 2가 들어가게 된다. 이는 길이가 1인 증가 부분 수열이 {5}와 {2}가 있는데 이 수열 중에서 끝 값이 더 작은 2를 x 배열에 저장해 놓는다는 의미이다.
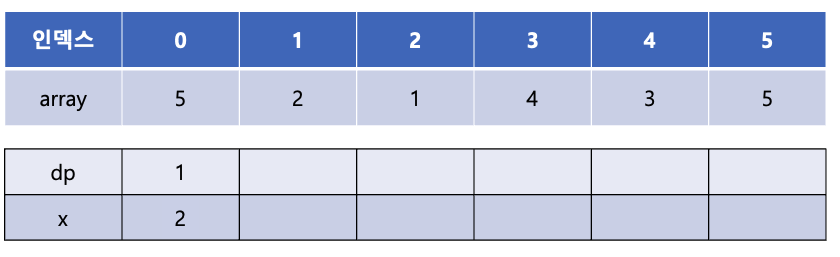
이제 array[2]의 값인 1을 살펴 보면 역시 x의 0번째에 들어갈 수 있고 이는 현재 x[0]의 값인 2보다 작기 때문에 x[0]을 1로 갱신해준다.
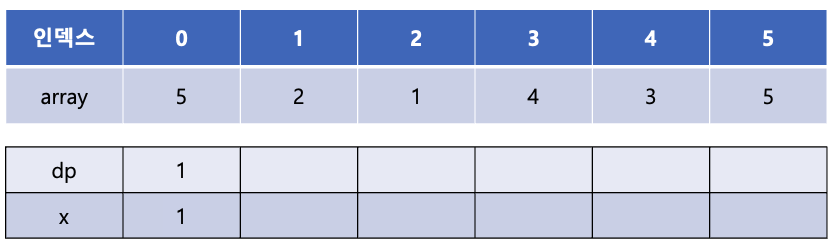
array[3]의 값인 4는 x 배열의 마지막 값인 1보다 크므로 새롭게 x 배열에 추가해 줄 수 있다. x[1]에 4를 추가해 주고 dp[1]에는 dp[0] + 1인 값 1을 넣어준다. 이는 증가 부분 수열의 길이가 2인 수열 중 끝이 4로 끝나는 수열이 있다는 것을 의미한다.
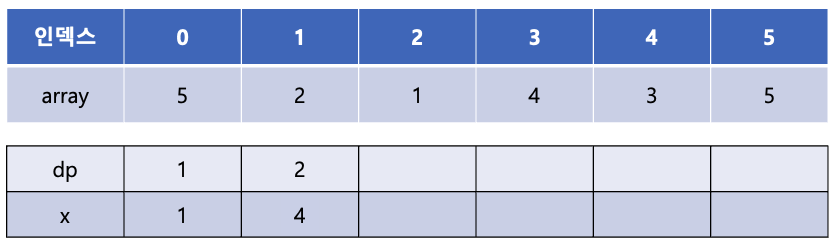
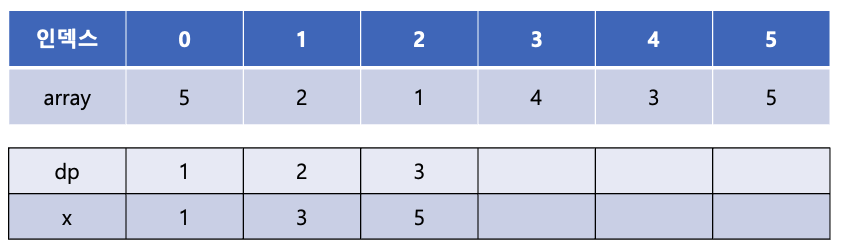
array[4]의 값인 3은 x 배열에서 1번째 인덱스에 들어갈 수 있으며 현재 x[1]의 값인 4보다 작다. x[1]의 값을 3으로 갱신해 준다. 이는 증가 부분 수열의 길이가 2인 수열 중 끝이 4와 3인 수열 중 더 작은 값인 3을 x 배열에 저장해 놓는다는 의미이다.

마지막으로 array[5]의 값인 5를 x 배열의 몇 번째에 넣을 수 있는지를 이분탐색을 통해 찾는다. x 배열의 마지막 값인 3보다 크므로 x 배열에 새롭게 5를 추가해 주고 dp 배열에는 dp 배열의 마지막 값에 + 1을 해주어 3을 추가해준다. 이는 증가 부분 수열의 길이가 3인 수열 중 끝이 5인 수열이 있다는 것을 의미한다.
이렇게 array의 마지막 까지 탐색을 끝내고 나면 위와 같이 dp 배열과 x 배열이 완성되고 이를 통해 LIS의 길이는 3이라는 것을 알 수 있다. x 배열은 항상 오름차순으로 정렬 되어 있기 때문에 array의 값이 x 배열의 어느 위치에 들어갈 수 있는지를 이분 탐색을 활용하여 찾을 수 있다.
소스코드
#include <iostream>
#include <vector>
using namespace std;
vector<int> v{ 5, 2, 1, 4, 3, 5 };
int BinarySearch(int s, int e, int val)
{
while (s < e)
{
int mid = (s + e) / 2;
if (v[mid] < val)
s = mid + 1;
else
e = mid;
}
return e;
}
int LIS_BS()
{
int ret = 0;
vector<int> lis;
lis.push_back(v[0]);
for (int i = 1; i < v.size(); i++)
{
//만약 lis 벡터의 마지막 수보다 i번째 수가 크다면, 그냥 뒤에 붙인다.
if (v[i] > lis.back())
{
lis.push_back(v[i]);
ret = lis.size() - 1;
}
//i번째 수에 대해, lis 벡터 내에서 그 수의 위치를 찾는다.
int pos = BinarySearch(0, ret, v[i]);
lis[pos] = v[i];
}
return ret + 1;
}
[Algorithm] 최장 증가 부분 수열 (LIS) (tistory.com)
최장 증가 수열 (LIS, Longest Increasing Subsequence) (tistory.com)
'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| 벨만 포드 (Bellman-Ford) 알고리즘 (0) | 2023.10.16 |
|---|---|
| DP(동적계획법)을 이용한 이항계수 (Binomial Coefficient) (0) | 2023.10.15 |
| [C++] STL container 시간 복잡도 및 특징 비교 (0) | 2023.10.10 |
| [알고리즘] 순열과 조합의 차이 (0) | 2023.10.09 |
| 카라츠바의 빠른 곱셈 (Karatsuba algorithm) (0) | 2023.10.08 |
