I. 다이나믹 프로그래밍
다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법이다.
이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다는 것이 핵심이다. 즉, 하나의 문제는 단 한 번만 풀도록 하는 알고리즘이다.
(우리가 평소에 문제를 풀이할 때 효율적인 방법으로 고안할 필요가 있다.)
다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(탑다운-하향식, 바텀업-상향식)으로 구성된다.
매우 비효율적인 문제더라도 다이나믹으로 획기적으로 시간을 줄일 수 있다.
다이나믹 프로그래밍은 조건을 만족해야 사용할 수 있다.
최적 부분 구조 - 큰 문제를 작은 문제로 나눌 수 있고, 작은 문제를 모아서 큰 문제를 해결
중복 부분 문제 - 동일한 작은 문제를 반복적으로 해결한다.
II. 피보나치 수열
피보나치 수열은 다이나믹 프로그래밍으로 효과적으로 계산할 수 있다.
각각의 피보나치 수열은 앞부분의 합이다.
이는 점화식을 통해 인접한 항들 사이의 관계식을 만들 수 있다.

피보나치 수열은 수열을 배열, 리스트로 표현하는 방식을 통해 선형적인 데이터를 만드는 재귀함수로 만들 수 있다.
피보나치 수열 계산과정은 그림으로 보면 각각을 구하기 위해 무엇이 필요한지 알 수 있다.
재귀함수로 간단하게 호출할 수 있고, 재귀함수의 종료조건을 명시해야 한다.

III. 피보나치 수열 : 단순 재귀 소스코드 (C++)
그러나 재귀함수로 풀이하면 지수 시간 복잡도를 가지게 된다. 즉, 여러번 호출되는 문제로 '중복되는 부분' 문제가 생긴다.
피보나치 수열은 너무 많은 시간 복잡도가 요구되는데 이를 다이나믹 프로그래밍으로 풀면 효율적이다. 또한 사용 조건에도 맞다. (최적 부분 구조, 중복 부분 문제)
#include <iostream>
using namespace std;
int fibo(int x){
if(x==1 || x==2){
return 1;
}
return fibo(x-1)+fibo(x-2);
}
int main(){
cout << fibo(4) << '\n';
return 0;
}IV. 하향식 (메모이제이션-Memoization)
메모이제이션(하향식)은 다이나믹 프로그래밍을 구현하는 방법이고, 이미 구한 답을 잠깐 저장해두는 것을 의미한다. 값을 기록해 놓는 점에서 캐싱(Caching)이라고도 한다.
V. 탑다운 VS 바텀업
하향식 -> 탑다운. 재귀함수. 큰 문제를 위해 작은 문제를 호출한다.
상향식 -> 보텀업. 먼저 계산한 값을 통해서 반복문을 이용한다.
결과 저장용 리스트는 DP 테이블이라고 부른다. 따라서 메모이제이션은 다이나믹 프로그래밍에 국한된 개념은 아니다.
// Memoization 탑다운 방식
#include <iostream>
using namespace std;
// 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 리스트 초기화
long long d[100];
// 피보나치 함수를 재귀함수로 구현(탑다운 다이나믹 프로그래밍)
int fibo(int x) {
// 종료조건(1혹은 2일때 1반환)
if(x==1 || x==2){
return 1;
}
// 이미 계산한적 있는 문제라면 그대로 반환
if(d[x] != 0) {
return d[x];
}
// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
return d[x] = fibo(x-1) + fibo(x-2);
}
int main() {
int N;
cin >> N;
cout << fibo(N);
}// 바텀업 방식
#include <iostream>
using namespace std;
// 앞서 계산된 결과를 저장하기 위한 DP테이블 초기화
long long d[100];
int main(void){
// 첫번째, 두번째 피보나치 수열은 1
d[1] = 1;
d[2] = 1;
int n = 50;
// 피보나치 함수 반복문으로 구현 (바텀업 다이나믹 프로그래밍)
for(int i=3; i<n+1; i++){
d[i] = d[i-1]+d[i-2];
}
cout << d[n] << '\n';
return 0;
}VI. 메모이제이션 동작 분석
이미 계산된 결과를 메모리에 저장하면 색칠된 노드만 처리할 것을 기대할 수 있다.
지수 시간 만큼 걸리던 피보나치 수열 문제를 시간복잡도 O(N)으로 만들 수 있다.
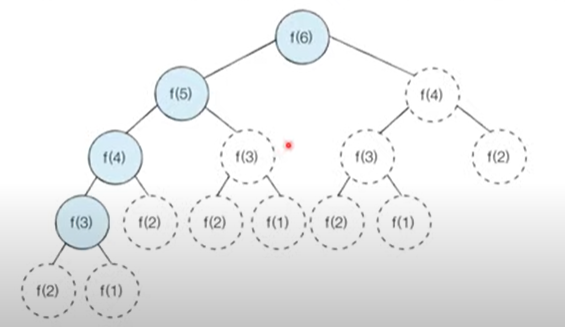
공통점 : 모두 최적 부분 구조를 가질 때 사용 가능
(큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 상황)
차이점 : 부분 문제 정복.
(다이나믹 프로그래밍 문제에서는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복되고,
분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않는다.)
분할 정복의 대표 사례인 퀵 정렬에서는 한 번 기준 원소가 자리를 변경해서 자리를 잡으면, 그 기준 원소의 위치가 바뀌지 않는다. 또한 분할 이후에 해당 피벗을 다시 처리하는 부분에서 다시 호출하지 않는다.
IX. 다이나믹 프로그래밍 접근 방법
문제가 다이나믹 프로그래밍 유형인지 파악하는 것이 중요하다. 즉, 문제의 풀이 방법을 고안하는 것이 먼저이다.
우선은 재귀함수로 비효율적인 코드를 작성한 뒤에 작은 문제에서 구한 답이 큰 문제에서 적용 가능하다면 코드 개선으로 다이나믹 프로그래밍을 사용할 수 있다. 또한 다이나믹 프로그래밍은 면접 과정에서 쉬운 난이도로 나올 수 있는 문제이다. 이미 해결한 문제를 반복적으로 해결하여 비효율적인 문제에서 유용할 것이다.
'CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘] 순열과 조합의 차이 (0) | 2023.10.09 |
|---|---|
| 카라츠바의 빠른 곱셈 (Karatsuba algorithm) (0) | 2023.10.08 |
| 탐욕 / 그리디 알고리즘 (Greedy Algorithm) (0) | 2023.10.06 |
| [C++] 이분 탐색 (Binary Search) (0) | 2023.10.05 |
| C++ MST 크루스칼 + 프림 알고리즘 코드 (0) | 2023.10.05 |
![[C++] Dynamic Programming (동적계획법) / Top-Down (탑다운)과 Bottom-Up (바텀업) 방식](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FUosSl%2Fbtsw6WzbCwO%2FCT9z5yukvVkOHp1RmGMWc1%2Fimg.png)