[DX11 물방울책] 챕터 1 - 벡터
벡터는 게임 그래픽스에서 아주 중요한 역할을 하고있다. 예) 충돌 처리 그리고 물리 작용.
1. 벡터란 무엇인가?
크기와 방향을 지닌 값이다. 예시는 아래와 같다.
- 강체 : 힘
- 위치
- 속도 : 가속도와 방향


2. 벡터와 좌표계
벡터를 좌표계로 표현할려면 현재 공간상 위치값을 치환하면 된다. 예) 3D (x, y, z), 2D (x,y)

두 프레임 즉 시점에 따라 같은 방향이어도 위치가 다를 수가 있다.

3. 왼손 좌표계 vs 오른손 좌표계
Direct3D는 왼손 좌표계를 사용한다.

4. 기본 벡터 연산
- 두 벡터는 모든 좌표가 일치해야 똑같다라고 할 수가 있다.
- 두 벡터간 덧셈은 오직 같은 좌표로만 진행한다.
- 스칼라곱 같은 경우엔 자연수를 각 좌표를 곱해야한다 (형태 유지).
- 두 벡터간 뺄셈은 (왼쪽 벡터 - 오른쪽 벡터) 여야 한다.

5. 길이와 단위 벡터
크기 정도는 벡터가 가리키고 있는 방향의 총 길이라고 볼 수가 있다.

6. 직교화
두 개의 벡터가 동일한 크기와 단위 벡터라면 직교한다고 볼 수가 있다.


7. 내적 (Dot Product / Scalar) 각도
내적은 벡터의 특정 방향, 성분, 투영(사영)의 크기, 일의 크기, 전류 밀도에 대한 전류의 크기 등을 구할 때 필요하다.
간단히 말하면 임의의 벡터의 특정 방향을 가진 성분의 크기를 알아내는데 유용하다는 것이다.
내적은 스칼라곱(scalar product) 또는 dot product라고도 말하며, 두 벡터의 크기와 두 벡터 사이의 각의 코사인 값을 곱한것으로 정의한다. (결과는 스칼라양이 나온다).
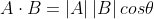
그리고 단위벡터를 이용하면 다른 방법으로 내적을 구할 수 있다.
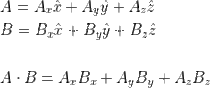
내적은 교환법칙이 성립한다.


8. 외적 (Cross Product)
외적은 면 벡터의 표현, 토크, 각속도등을 구할때 필요하다.
외적은 두 벡터에 수직인 벡터를 구한다던지, 한 평면의 법선벡터(수직인벡터)를 구할 때 유용하다.
외적은 벡터곱(vector product) 또는 cross product라고 말하며, 두 벡터의 크기와 두 벡터 사이의 각의 사인값 그리고 수직인 벡터의 곱으로 정의한다. (결과는 벡터값이 나온다).


9. 위치
그래픽스에서 위치를 명시하는건 필수이다. 예로 들어서 물체의 위치라던지 카메라의 위치.


#include <iostream>
#include <d3d11.h>
#include <d3dx11.h>
#include <xnamath.h> // 연산 코드를 사용하기 위해선 필수
using namespace std;
int main()
{
// 2D 좌표
XMFLOAT2 twoD_val(5.5f, 2.2f);
XMVECTOR twoD_pos = XMLoadFloat2(&twoD_val);
// 3D 좌표
XMFLOAT3 threeD_val(1.2f, 2.3f, 4.f);
XMVECTOR threeD_pos = XMLoadFloat3(&threeD_val);
// 쿼터니언
XMFLOAT4 quaternionVal(2.5f, 3.3f, 1.1f, 2.f);
XMVECTOR quaternionPos = XMLoadFloat4(&quaternionVal);
// 출력
cout << "PosX : " << XMVectorGetX(twoD_pos) << " PosY : " << XMVectorGetY(twoD_pos) << endl;
cout << "PosX : " << XMVectorGetX(threeD_pos) << " PosY : " << XMVectorGetY(threeD_pos) << " PosZ : " << XMVectorGetZ(threeD_pos) << endl;
cout << "PosX : " << XMVectorGetX(quaternionPos) << " PosY : " << XMVectorGetY(quaternionPos) << " PosZ : " << XMVectorGetZ(quaternionPos) << " PosW : " << XMVectorGetW(quaternionPos) << endl;
// 단일벡터
auto singleVec = XMVector4Normalize(quaternionPos);
cout << "단일벡터 값) PosX : " << XMVectorGetX(singleVec) << " PosY : " << XMVectorGetY(singleVec) << " PosZ : " << XMVectorGetZ(singleVec) << endl;
// 내적
auto dotVal = XMVector4Dot(twoD_pos, threeD_pos);
cout << "내적 값) PosX : " << XMVectorGetX(dotVal) << " PosY : " << XMVectorGetY(dotVal) << " PosZ : " << XMVectorGetZ(dotVal) << endl;
// 외적
auto crossProduct = XMVector4Cross(twoD_pos, threeD_pos, quaternionPos);
cout << "외적 값) PosX : " << XMVectorGetX(crossProduct) << " PosY : " << XMVectorGetY(crossProduct) << " PosZ : " << XMVectorGetZ(crossProduct) << endl;
}